CosmicOS full message

0	introduce numbers (in unary notation)	MATH
1	introduce equality for unary numbers	MATH
2	now introduce other relational operators	MATH
3	introduce the NOT logical operator	MATH
4	introduce addition	MATH
5	introduce subtraction	MATH
6	introduce multiplication	MATH
7	introduce a simple form of binary notation	MATH
8	show local assignment	MATH
9	demonstrate existence of memory	MATH
10	use equality for truth values	MATH
11	show mechanisms for branching	MATH
12	introduce the AND logical operator	MATH
13	introduce the OR logical operator	MATH
14	illustrate pairs	MATH
15	introduce mutable objects, and side-effects	MATH
16	illustrate lists and some list operators	MATH
17	describe changes to the implicit interpreter to allow new special forms	HACK
18	introduce sugar for let	MATH
19	build up functions of several variables	MATH
20	show map function for applying a function across the elements of a list	MATH
21	end of part 1, start of part 2	NOTE
22	show an example of recursive evaluation	MATH
23	some pure lambda calculus definitions - optional	MATH
24	introduce universal quantifier	MATH
25	introduce existential quantifier	MATH
26	introduce logical implication	MATH
27	introduce sets and set membership	MATH
28	introduce graph structures	MATH
29	show how to execute a sequence of instructions	MATH
30	introduce environment/hashmap structure	MATH
31	introduce simple mutable structures	OBJECT
32	introduce method handler wrappers	OBJECT
33	introduce turing machine model	TURING
34	introduce simple form of typing, for ease of documentation.	OBJECT
35	an example object -- a 2D point	OBJECT
36	an example object -- a container	OBJECT
37	expressing inheritance	OBJECT
38	adding a special form for classes	OBJECT
39	wrapper class for cells	OBJECT
40	playing around with doors and rooms	MUD
41	end of part 2, start of part 3	NOTE
42	simulating unless gates	GATE
43	testing alternate primer based on gates: cos_not circuit	GATE
44	testing alternate primer based on gates: cos_and circuit	GATE
45	testing alternate primer based on gates: cos_or circuit	GATE
46	testing alternate primer based on gates: cos_nor circuit	GATE
47	testing alternate primer based on gates: cos_osc circuit	GATE
48	testing alternate primer based on gates: cos_sr circuit	GATE
49	testing alternate primer based on gates: cos_d circuit	GATE
50	probing networks of unless gates	GATE
51	end of part 3, start of part 4	NOTE
52	a mechanism for referring to parts of the message	SELF
53	some preparatory work for integrating with Java code	JAVA
54	class translation 'COS_JavaTest'	JAVA
55	check that automatic conversion is workable	JAVA
56	another simple little text-adventure space	MUD
57	native implementation of a Java list, hash classes	JAVA
58	testing the JList class	JAVA
59	basic iterator implementation	JAVA
60	class translation 'COS_JDoor'	JAVA
61	class translation 'COS_JThing'	JAVA
62	class translation 'COS_JRoom'	JAVA
63	class translation 'COS_JNamed'	JAVA
64	class translation 'COS_JWorld'	JAVA
65	class translation 'COS_JRobo'	JAVA
66	test JRoom, JDoor, JThing, etc	JAVA

#   Author: Paul Fitzpatrick, paulfitz@csail.mit.edu
#   Copyright (c) 2005 Paul Fitzpatrick
#
#   This file is part of CosmicOS.
#
#   CosmicOS is free software; you can redistribute it and/or modify
#   it under the terms of the GNU General Public License as published by
#   the Free Software Foundation; either version 2 of the License, or
#   (at your option) any later version.
#
#   CosmicOS is distributed in the hope that it will be useful,
#   but WITHOUT ANY WARRANTY; without even the implied warranty of
#   MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE.  See the
#   GNU General Public License for more details.
#
#   You should have received a copy of the GNU General Public License
#   along with CosmicOS; if not, write to the Free Software
#   Foundation, Inc., 59 Temple Place, Suite 330, Boston, MA  02111-1307  USA
#

0. introduce numbers (in unary notation)

# Here we count up, go through some primes, etc.
# There is some syntax around the numbers, but that doesn't
# need to be understood at this point.
# Any 'words' written here are converted to arbitrary integers
# in the actual message.  Any word ending in -in-unary will be given
# in unary rather than the binary code used in the main body
# of the message.

intro-in-unary U1U;

intro-in-unary U11U;

intro-in-unary U111U;

intro-in-unary U1111U;

intro-in-unary U11111U;

intro-in-unary U111111U;

intro-in-unary U1111111U;

intro-in-unary U11111111U;

intro-in-unary U111111111U;

intro-in-unary U1111111111U;

intro-in-unary U11111111111U;

intro-in-unary U111111111111U;

intro-in-unary U1111111111111U;

intro-in-unary U11111111111111U;

intro-in-unary U111111111111111U;

intro-in-unary U1111111111111111U;

intro-in-unary U11U;

intro-in-unary U111U;

intro-in-unary U11111U;

intro-in-unary U1111111U;

intro-in-unary U11111111111U;

intro-in-unary U1111111111111U;

intro-in-unary U1U;

intro-in-unary U1111U;

intro-in-unary U111111111U;

intro-in-unary U1111111111111111U;

1. introduce equality for unary numbers

# The intro operator does nothing essential, and could be
# omitted - it just tags the first use of a new operator.
# The = operator is introduced alongside a duplication of
# unary numbers.  The meaning will not quite by nailed down
# until we see other relational operators.

=-in-unary U1U U1U;

=-in-unary U11U U11U;

=-in-unary U111U U111U;

=-in-unary U1111U U1111U;

=-in-unary U11111U U11111U;

=-in-unary U111111U U111111U;

=-in-unary U1111111U U1111111U;

=-in-unary U11111111U U11111111U;

=-in-unary U1U U1U;

=-in-unary U111111U U111111U;

=-in-unary U11U U11U;

2. now introduce other relational operators

# After this lesson, it should be clear what contexts
# < > and = are appropriate in.
# drive the lesson home

=-in-unary U1U U1U;

>-in-unary U11U U1U;

>-in-unary U111U U1U;

>-in-unary U1111U U1U;

<-in-unary U1U U11U;

=-in-unary U11U U11U;

>-in-unary U111U U11U;

>-in-unary U1111U U11U;

<-in-unary U1U U111U;

<-in-unary U11U U111U;

=-in-unary U111U U111U;

>-in-unary U1111U U111U;

<-in-unary U1U U1111U;

<-in-unary U11U U1111U;

<-in-unary U111U U1111U;

=-in-unary U1111U U1111U;

>-in-unary U1U UU;

>-in-unary U111111111U U11U;

>-in-unary U111111U UU;

>-in-unary U11U UU;

>-in-unary U11111111U U11U;

>-in-unary U1111U U1U;

>-in-unary U11U UU;

>-in-unary U1111111111U U1U;

>-in-unary U111111U U1U;

>-in-unary U111111111U U1U;

>-in-unary U1111111U U1U;

<-in-unary UU U1U;

<-in-unary U111U U1111111111U;

<-in-unary U1111U U111111111U;

<-in-unary U11U U1111U;

<-in-unary U1U U1111111U;

<-in-unary UU U1111111111U;

<-in-unary UU U11U;

<-in-unary UU U11U;

<-in-unary U1U U111U;

<-in-unary U11U U11111U;

<-in-unary U1U U1111U;

# switch to binary labelling for commands

= U1U U1U;

> U11U U1U;

> U111U U1U;

> U1111U U1U;

< U1U U11U;

= U11U U11U;

> U111U U11U;

> U1111U U11U;

< U1U U111U;

< U11U U111U;

= U111U U111U;

> U1111U U111U;

< U1U U1111U;

< U11U U1111U;

< U111U U1111U;

= U1111U U1111U;

# a few more random examples

< U111U U1111U;

= U1111U U1111U;

< U1U U11111U;

> U1111U UU;

> U11111U U1111U;

< U11U U111U;

> U11U U1U;

> U11111U U1U;

= U111U U111U;

= U111U U111U;

> U1U UU;

3. introduce the NOT logical operator

intro not;

= UU UU;

not / < UU UU;

not / > UU UU;

= U1111U U1111U;

not / < U1111U U1111U;

not / > U1111U U1111U;

= U111111U U111111U;

not / < U111111U U111111U;

not / > U111111U U111111U;

= U11U U11U;

not / < U11U U11U;

not / > U11U U11U;

= U111U U111U;

not / < U111U U111U;

not / > U111U U111U;

not / = U111U U1111111111U;

< U111U U1111111111U;

not / > U111U U1111111111U;

not / = U11111U U1111111U;

< U11111U U1111111U;

not / > U11111U U1111111U;

not / = U1U U11U;

< U1U U11U;

not / > U1U U11U;

not / = UU U11111U;

< UU U11111U;

not / > UU U11111U;

not / = U11111111U U11111111111111U;

< U11111111U U11111111111111U;

not / > U11111111U U11111111111111U;

not / = U11111111111U U111111U;

> U11111111111U U111111U;

not / < U11111111111U U111111U;

not / = U111111111111U U11U;

> U111111111111U U11U;

not / < U111111111111U U11U;

not / = U1111111111U U1111111U;

> U1111111111U U1111111U;

not / < U1111111111U U1111111U;

not / = U1111U UU;

> U1111U UU;

not / < U1111U UU;

not / = U1111111111111111U U111111111U;

> U1111111111111111U U111111111U;

not / < U1111111111111111U U111111111U;

4. introduce addition

intro +;

= U11U / + UU U11U;

= U11111U / + U1111U U1U;

= U11U / + U11U UU;

= U1111U / + UU U1111U;

= U1111U / + U111U U1U;

= U111U / + U1U U11U;

= UU / + UU UU;

= U1111U / + U1111U UU;

= U111U / + U11U U1U;

= U1111U / + U1111U UU;

5. introduce subtraction

intro -;

= UU / - U11U U11U;

= U1111U / - U11111U U1U;

= U11U / - U11U UU;

= UU / - U1111U U1111U;

= U111U / - U1111U U1U;

= U1U / - U111U U11U;

= UU / - UU UU;

= U1111U / - U1111U UU;

= U11U / - U111U U1U;

= U1111U / - U1111U UU;

6. introduce multiplication

intro *;

= UU / * UU UU;

= UU / * UU U1U;

= UU / * UU U11U;

= UU / * UU U111U;

= UU / * U1U UU;

= U1U / * U1U U1U;

= U11U / * U1U U11U;

= U111U / * U1U U111U;

= UU / * U11U UU;

= U11U / * U11U U1U;

= U1111U / * U11U U11U;

= U111111U / * U11U U111U;

= UU / * U111U UU;

= U111U / * U111U U1U;

= U111111U / * U111U U11U;

= U111111111U / * U111U U111U;

= UU / * UU U1U;

= U111U / * U111U U1U;

= UU / * U11U UU;

= UU / * UU U111U;

= U111U / * U111U U1U;

= U11U / * U1U U11U;

= UU / * UU UU;

= UU / * U111U UU;

= UU / * U11U UU;

= UU / * U111U UU;

7. introduce a simple form of binary notation

# After this lesson, in the higher-level version of the message,
# will expand decimal to stand for the binary notation given.
# It wouldn't be hard to accompany this lesson with a more
# formal definition once functions are introduced (below)
# so maybe the transition to binary should be delayed?

= (:) U1U;

= (:.) U11U;

= (:..) U1111U;

= (:...) U11111111U;

= (:....) U1111111111111111U;

= (.) UU;

= (:) U1U;

= (:.) U11U;

= (::) U111U;

= (:..) U1111U;

= (:.:) U11111U;

= (::.) U111111U;

= (:::) U1111111U;

= (:...) U11111111U;

= (:..:) U111111111U;

= (:.:.) U1111111111U;

= (:.::) U11111111111U;

= (::..) U111111111111U;

= (::.:) U1111111111111U;

= (:::.) U11111111111111U;

= (::::) U111111111111111U;

= (.) UU;

= (:::) U1111111U;

= (::.:) U1111111111111U;

= (:.:) U11111U;

= (:..:) U111111111U;

= (.) UU;

= (::) U111U;

= (::::) U111111111111111U;

= (::..) U111111111111U;

= (:.:) U11111U;

= (:.:) U11111U;

= (:..:) U111111111U;

= (:.) U11U;

= (:) U1U;

= (::::) U111111111111111U;

= (:.) U11U;

= U11111U / + U1111U U1U;

= (:.:) / + (:..) (:);

= U1111111U / + U111111U U1U;

= (:::) / + (::.) (:);

= U11111U / + U1111U U1U;

= (:.:) / + (:..) (:);

= U1111U / + UU U1111U;

= (:..) / + (.) (:..);

= U111111111U / + U1111111U U11U;

= (:..:) / + (:::) (:.);

= U11111111111U / + U1111111U U1111U;

= (:.::) / + (:::) (:..);

= U1111111111U / + U111U U1111111U;

= (:.:.) / + (::) (:::);

= U111111U / + U11111U U1U;

= (::.) / + (:.:) (:);

= U1111U / * U1111U U1U;

= (:..) / * (:..) (:);

= U1111U / * U1U U1111U;

= (:..) / * (:) (:..);

= U1111U / * U1U U1111U;

= (:..) / * (:) (:..);

= U111111U / * U11U U111U;

= (::.) / * (:.) (::);

= U111111U / * U11U U111U;

= (::.) / * (:.) (::);

= U1111U / * U11U U11U;

= (:..) / * (:.) (:.);

= U111111111U / * U111U U111U;

= (:..:) / * (::) (::);

= U1111111111111111U / * U1111U U1111U;

= (:....) / * (:..) (:..);

8. show local assignment

assign 20 0 / = (20) 0;

assign 20 1 / = (20) 1;

assign 20 2 / = (20) 2;

assign 21 0 / = (21) 0;

assign 21 1 / = (21) 1;

assign 21 2 / = (21) 2;

assign 22 0 / = (22) 0;

assign 22 1 / = (22) 1;

assign 22 2 / = (22) 2;

= 0 (assign 20 0 (20));

= 0 (assign 20 0 / 20);

= 0 / assign 20 0 / 20;

= 20 / assign 20 0 20;

= 5 / assign 20 0 5;

= 5 / assign 20 0 / assign 23 5 / 23;

= 23 / assign 20 0 / assign 23 5 23;

= 1 (assign 20 1 (20));

= 1 (assign 20 1 / 20);

= 1 / assign 20 1 / 20;

= 20 / assign 20 1 20;

= 5 / assign 20 1 5;

= 5 / assign 20 1 / assign 23 5 / 23;

= 23 / assign 20 1 / assign 23 5 23;

= 2 (assign 20 2 (20));

= 2 (assign 20 2 / 20);

= 2 / assign 20 2 / 20;

= 20 / assign 20 2 20;

= 5 / assign 20 2 5;

= 5 / assign 20 2 / assign 23 5 / 23;

= 23 / assign 20 2 / assign 23 5 23;

= 0 (assign 21 0 (21));

= 0 (assign 21 0 / 21);

= 0 / assign 21 0 / 21;

= 21 / assign 21 0 21;

= 5 / assign 21 0 5;

= 5 / assign 21 0 / assign 23 5 / 23;

= 23 / assign 21 0 / assign 23 5 23;

= 1 (assign 21 1 (21));

= 1 (assign 21 1 / 21);

= 1 / assign 21 1 / 21;

= 21 / assign 21 1 21;

= 5 / assign 21 1 5;

= 5 / assign 21 1 / assign 23 5 / 23;

= 23 / assign 21 1 / assign 23 5 23;

= 2 (assign 21 2 (21));

= 2 (assign 21 2 / 21);

= 2 / assign 21 2 / 21;

= 21 / assign 21 2 21;

= 5 / assign 21 2 5;

= 5 / assign 21 2 / assign 23 5 / 23;

= 23 / assign 21 2 / assign 23 5 23;

= 0 (assign 22 0 (22));

= 0 (assign 22 0 / 22);

= 0 / assign 22 0 / 22;

= 22 / assign 22 0 22;

= 5 / assign 22 0 5;

= 5 / assign 22 0 / assign 23 5 / 23;

= 23 / assign 22 0 / assign 23 5 23;

= 1 (assign 22 1 (22));

= 1 (assign 22 1 / 22);

= 1 / assign 22 1 / 22;

= 22 / assign 22 1 22;

= 5 / assign 22 1 5;

= 5 / assign 22 1 / assign 23 5 / 23;

= 23 / assign 22 1 / assign 23 5 23;

= 2 (assign 22 2 (22));

= 2 (assign 22 2 / 22);

= 2 / assign 22 2 / 22;

= 22 / assign 22 2 22;

= 5 / assign 22 2 5;

= 5 / assign 22 2 / assign 23 5 / 23;

= 23 / assign 22 2 / assign 23 5 23;

# Now for functions.

assign 20 (? 28 5) / = 5 (20 2);

assign 32 (? 24 5) / = 5 (32 3);

assign 28 (? 29 6) / = 6 (28 2);

assign 30 (? 32 6) / = 6 (30 3);

assign 25 (? 38 (38)) / = 2 (25 2);

assign 23 (? 30 (30)) / = 3 (23 3);

assign 25 (? 33 (33)) / = 2 (25 2);

assign 29 (? 21 (21)) / = 3 (29 3);

assign 25 (? 32 / + (32) 1) / = 3 (25 2);

assign 31 (? 38 / + (38) 1) / = 4 (31 3);

assign 35 (? 33 / + (33) 1) / = 3 (35 2);

assign 32 (? 26 / + (26) 1) / = 4 (32 3);

assign y (? x / + (x) 6) / = (y 6) 12;

= ((? x / + (x) 6) 6) 12;

assign y (? x / + (x) 4) / = (y 0) 4;

= ((? x / + (x) 4) 0) 4;

assign y (? x / + (x) 12) / = (y 0) 12;

= ((? x / + (x) 12) 0) 12;

assign y (? x / + (x) 15) / = (y 2) 17;

= ((? x / + (x) 15) 2) 17;

assign z (? x / ? y / + 1 / * (x) (y)) / = (z 13 4) 53;

assign z (? x / ? y / + 1 / * (x) (y)) / = ((z 13) 4) 53;

= ((? x / ? y / + 1 / * (x) (y)) 13 4) 53;

= (((? x / ? y / + 1 / * (x) (y)) 13) 4) 53;

assign z (? x / ? y / + 1 / * (x) (y)) / = (z 5 6) 31;

assign z (? x / ? y / + 1 / * (x) (y)) / = ((z 5) 6) 31;

= ((? x / ? y / + 1 / * (x) (y)) 5 6) 31;

= (((? x / ? y / + 1 / * (x) (y)) 5) 6) 31;

assign z (? x / ? y / + 1 / * (x) (y)) / = (z 7 8) 57;

assign z (? x / ? y / + 1 / * (x) (y)) / = ((z 7) 8) 57;

= ((? x / ? y / + 1 / * (x) (y)) 7 8) 57;

= (((? x / ? y / + 1 / * (x) (y)) 7) 8) 57;

assign z (? x / ? y / + 1 / * (x) (y)) / = (z 8 2) 17;

assign z (? x / ? y / + 1 / * (x) (y)) / = ((z 8) 2) 17;

= ((? x / ? y / + 1 / * (x) (y)) 8 2) 17;

= (((? x / ? y / + 1 / * (x) (y)) 8) 2) 17;

assign w (? x / ? y / ? z / = (z) / + (x) (y)) / w 15 14 29;

assign w (? x / ? y / ? z / = (z) / + (x) (y)) / w 5 8 13;

assign w (? x / ? y / ? z / = (z) / + (x) (y)) / w 12 15 27;

assign w (? x / ? y / ? z / = (z) / + (x) (y)) / w 14 14 28;

assign w (? x / ? y / ? z / = (z) / + (x) (y)) / w 8 0 8;

assign w (? x / ? y / ? z / = (z) / + (x) (y)) / w 15 9 24;

assign w (? x / ? y / ? z / = (z) / + (x) (y)) / w 11 15 26;

assign w (? x / ? y / ? z / = (z) / + (x) (y)) / w 5 7 12;

9. demonstrate existence of memory

define forty-something 42;

= 42 (forty-something);

# now introduce a function

assign square (? x / * (x) (x)) / = 0 (square 0);

assign square (? x / * (x) (x)) / = 16 (square 4);

assign square (? x / * (x) (x)) / = 64 (square 8);

assign square (? x / * (x) (x)) / = 9 (square 3);

# show that functions can be remembered across statements

define square / ? x / * (x) (x);

= (square 5) 25;

= (square 0) 0;

= (square 1) 1;

= (square 9) 81;

define plusone / ? x / + (x) 1;

= (plusone 7) 8;

= (plusone 3) 4;

= (plusone 3) 4;

= (plusone 5) 6;

10. use equality for truth values

= (= U11U U11U) (> U1111U U11U);

= (= U1U U1U) (> U111111U U1111U);

= (< U111U U1111U) (= U11111U U11111U);

= (= U111U U111U) (= U1111U U1111U);

= (= U111U U111U) (= UU UU);

= (< U111111U U11U) (< U1111U U11U);

= (< U1111U U1U) (> UU UU);

= (> UU U11111U) (= U111U U11U);

= (> U11U U111U) (> U1111U U11111U);

= (> U11U U111111U) (> U1U U111111U);

not / = (> U11U U111U) (< U1U U1111U);

not / = (= U1111U U111U) (< U1U U11U);

not / = (= U11111U U1111U) (< U11U U1111U);

not / = (> U1111U U111111U) (= U111U U111U);

not / = (= U111U U1U) (> U1111U U1U);

not / = (< U111U U111111U) (< U111111U U11U);

not / = (= U11U U11U) (> U11U U11111U);

not / = (= U11111U U11111U) (< U111111U U11U);

not / = (= U111U U111U) (< U1111U U111U);

not / = (> U11111U U11U) (< U11111U U1111U);

# This could all be simplified or removed
# once the handling of true/false stabilizes

define true 1;

define false 0;

= (true) (= U1U U1U);

= (true) (= UU UU);

= (true) (> U1111111U U11111U);

= (true) (= U11111U U11111U);

= (true) (= U1111U U1111U);

= (< U11111U U111111U) (true);

= (= U11111U U11111U) (true);

= (> U1111111U U11111U) (true);

= (= U11U U11U) (true);

= (< U111U U111111U) (true);

= (false) (< U11111U UU);

= (false) (= U11U U111U);

= (false) (< U111111U U11U);

= (false) (> U1U U11U);

= (false) (> U11U U11111U);

= (= U1111U U111U) (false);

= (= UU U1U) (false);

= (< U111111U U111U) (false);

= (= U111U UU) (false);

= (= U1111U U111U) (false);

= (true) (true);

= (false) (false);

not / = (true) (false);

not / = (false) (true);

11. show mechanisms for branching

intro if;

= 28 / if (< 3 0) 24 28;

= 27 / if (> 2 4) 29 27;

= 29 / if (= 3 1) 20 29;

= 21 / if (= 0 0) 21 26;

= 29 / if (> 5 3) 29 23;

= 26 / if (> 1 0) 26 22;

= 21 / if (= 3 3) 21 27;

= 23 / if (> 4 4) 25 23;

define max / ? x / ? y / if (> (x) (y)) (x) (y);

define min / ? x / ? y / if (< (x) (y)) (x) (y);

= 0 / max 0 0;

= 0 / min 0 0;

= 1 / max 0 1;

= 0 / min 0 1;

= 2 / max 0 2;

= 0 / min 0 2;

= 1 / max 1 0;

= 0 / min 1 0;

= 1 / max 1 1;

= 1 / min 1 1;

= 2 / max 1 2;

= 1 / min 1 2;

= 2 / max 2 0;

= 0 / min 2 0;

= 2 / max 2 1;

= 1 / min 2 1;

= 2 / max 2 2;

= 2 / min 2 2;

# need to be careful about whether 'if' is eager or lazy
# here we suggest that it is lazy

define factorial / ? n / if (< (n) 1) 1 / * (n) / factorial / - (n) 1;

= 1 / factorial 1;

= 2 / factorial 2;

= 6 / factorial 3;

= 24 / factorial 4;

= 120 / factorial 5;

12. introduce the AND logical operator

intro and;

define and (? x / ? y / if (x) (if (y) (true) (false)) (false));

and (= U11U U11U) (> U1111U U11U);

and (= U1U U1U) (> U111111U U1111U);

and (< U111U U1111U) (= U11111U U11111U);

and (= U111U U111U) (= U1111U U1111U);

and (= U111U U111U) (= UU UU);

and (< U11111U U1111111U) (> U11111U U111U);

and (> U11111U U1111U) (> U1U UU);

and (> U111U UU) (= U111U U111U);

and (< U111U U1111U) (< U111U U111111U);

and (> U11111U U1111U) (> U11111U U1111U);

not / and (> U111111U U1111U) (< U111U U1U);

not / and (> U111U U1U) (> U111U U111U);

not / and (= UU UU) (= U11111U U1111U);

not / and (< U11U U1111U) (> U1111U U111111U);

not / and (= U111U U111U) (= U111U U1U);

not / and (> U1U U11111U) (< U111U U111111U);

not / and (< U111111U U11U) (= U11U U11U);

not / and (> U11U U11111U) (= U11111U U11111U);

not / and (< U111111U U11U) (= U111U U111U);

not / and (< U1111U U111U) (> U11111U U11U);

not / and (< U11111U U1111U) (= U1U U11U);

not / and (< U111111U U1111U) (= U11111U U1U);

not / and (> U11U U111111U) (= U1U U11111U);

not / and (< U111111U U111U) (= U11U U111U);

not / and (< U111111U U1111U) (> UU U1U);

not / and (= U111U U11111U) (< U1111U U1U);

not / and (= U1111U U1U) (< U1111U U11U);

not / and (< U111111U U111U) (= U111U UU);

not / and (< U1111U U11U) (< U1111U U111111U);

not / and (> U1111U U1U) (< U11111U U11U);

not / and (> UU U1U) (> U1111111U U11111U);

not / and (< U111U U1111U) (> U111U U111111U);

not / and (> U1U U11U) (> U111111U U1111U);

not / and (< UU U1U) (= U1111U U11111U);

and (< U1111U U111111U) (< U11111U U1111111U);

13. introduce the OR logical operator

define or (? x / ? y / if (x) (true) (if (y) (true) (false)));

intro or;

or (= U11U U11U) (> U1111U U11U);

or (= U1U U1U) (> U111111U U1111U);

or (< U111U U1111U) (= U11111U U11111U);

or (= U111U U111U) (= U1111U U1111U);

or (= U111U U111U) (= UU UU);

or (< U11111U U1111111U) (> U11111U U111U);

or (> U11111U U1111U) (> U1U UU);

or (> U111U UU) (= U111U U111U);

or (< U111U U1111U) (< U111U U111111U);

or (> U11111U U1111U) (> U11111U U1111U);

or (> U111111U U1111U) (< U111U U1U);

or (> U111U U1U) (> U111U U111U);

or (= UU UU) (= U11111U U1111U);

or (< U11U U1111U) (> U1111U U111111U);

or (= U111U U111U) (= U111U U1U);

or (> U1U U11111U) (< U111U U111111U);

or (< U111111U U11U) (= U11U U11U);

or (> U11U U11111U) (= U11111U U11111U);

or (< U111111U U11U) (= U111U U111U);

or (< U1111U U111U) (> U11111U U11U);

not / or (< U11111U U1111U) (= U1U U11U);

not / or (< U111111U U1111U) (= U11111U U1U);

not / or (> U11U U111111U) (= U1U U11111U);

not / or (< U111111U U111U) (= U11U U111U);

not / or (< U111111U U1111U) (> UU U1U);

not / or (= U111U U11111U) (< U1111U U1U);

not / or (= U1111U U1U) (< U1111U U11U);

not / or (< U111111U U111U) (= U111U UU);

or (< U1111U U11U) (< U1111U U111111U);

or (> U1111U U1U) (< U11111U U11U);

or (> UU U1U) (> U1111111U U11111U);

or (< U111U U1111U) (> U111U U111111U);

or (> U1U U11U) (> U111111U U1111U);

or (< UU U1U) (= U1111U U11111U);

or (< U1111U U111111U) (< U11111U U1111111U);

define >= (? x / ? y / or (> (x) (y)) (= (x) (y)));

define <= (? x / ? y / or (< (x) (y)) (= (x) (y)));

>= 0 0;

<= 0 0;

not / >= 0 1;

<= 0 1;

not / >= 0 2;

<= 0 2;

>= 1 0;

not / <= 1 0;

>= 1 1;

<= 1 1;

not / >= 1 2;

<= 1 2;

>= 2 0;

not / <= 2 0;

>= 2 1;

not / <= 2 1;

>= 2 2;

<= 2 2;

14. illustrate pairs

define cons (? x / ? y / ? f / f (x) (y));

define car (? pair / pair (? x / ? y / x));

define cdr (? pair / pair (? x / ? y / y));

assign x (cons 0 4) / = (car / x) 0;

assign x (cons 0 4) / = (cdr / x) 4;

assign x (cons 6 2) / = (car / x) 6;

assign x (cons 6 2) / = (cdr / x) 2;

assign x (cons 3 9) / = (car / x) 3;

assign x (cons 3 9) / = (cdr / x) 9;

assign x (cons 7 / cons 10 2) / = (car / x) 7;

assign x (cons 7 / cons 10 2) / = (car / cdr / x) 10;

assign x (cons 7 / cons 10 2) / = (cdr / cdr / x) 2;

assign x (cons 1 / cons 15 17) / = (car / x) 1;

assign x (cons 1 / cons 15 17) / = (car / cdr / x) 15;

assign x (cons 1 / cons 15 17) / = (cdr / cdr / x) 17;

assign x (cons 8 / cons 14 9) / = (car / x) 8;

assign x (cons 8 / cons 14 9) / = (car / cdr / x) 14;

assign x (cons 8 / cons 14 9) / = (cdr / cdr / x) 9;

assign x (cons 3 / cons 0 / cons 2 / cons 4 1) / and (= 3 / car / x) / and (= 0 / car / cdr / x) / and (= 2 / car / cdr / cdr / x) / and (= 4 / car / cdr / cdr / cdr / x) (= 1 / cdr / cdr / cdr / cdr / x);

15. introduce mutable objects, and side-effects

intro make-cell;

intro set!;

intro get!;

define demo-mut1 / make-cell 0;

set! (demo-mut1) 15;

= (get! / demo-mut1) 15;

set! (demo-mut1) 5;

set! (demo-mut1) 7;

= (get! / demo-mut1) 7;

define demo-mut2 / make-cell 11;

= (get! / demo-mut2) 11;

set! (demo-mut2) 22;

= (get! / demo-mut2) 22;

= (get! / demo-mut1) 7;

= (+ (get! / demo-mut1) (get! / demo-mut2)) 29;

if (= (get! / demo-mut1) 7) (set! (demo-mut1) 88) (set! (demo-mut1) 99);

= (get! / demo-mut1) 88;

if (= (get! / demo-mut1) 7) (set! (demo-mut1) 88) (set! (demo-mut1) 99);

= (get! / demo-mut1) 99;

16. illustrate lists and some list operators

# to make list describable as a function, need to preceed lists
# ... with an argument count
# Lists keep an explicit record of their length
# this is to avoid the need for using a special 'nil' symbol
# ... which cannot itself be placed in the list.
# pending: should introduce number? check function

define list-helper / ? n / ? ret / if (> (n) 1) (? x / list-helper (- (n) 1) (? y / ? z / ret (+ 1 (y)) (cons (x) (z)))) (? x / ret 1 (x));

define list / ? n / if (= (n) 0) (cons 0 0) (list-helper (n) (? y / ? z / cons (y) (z)));

define head / ? lst / if (= (car / lst) 0) (undefined) (if (= (car / lst) 1) (cdr / lst) (car / cdr / lst));

define tail / ? lst / if (= (car / lst) 0) (undefined) (if (= (car / lst) 1) (cons 0 0) (cons (- (car / lst) 1) (cdr / cdr / lst)));

define list-length / ? lst / car / lst;

define list-ref / ? lst / ? n / if (= (list-ref / lst) 0) (undefined) (if (= (n) 0) (head / lst) (list-ref (tail / lst) (- (n) 1)));

define prepend / ? x / ? lst / if (= (list-length / lst) 0) (cons 1 (x)) (cons (+ (list-length / lst) 1) (cons (x) (cdr / lst)));

define equal / ? x / ? y / if (= (number? (x)) (number? (y))) (if (number? (x)) (= (x) (y)) (list= (x) (y))) (false);

define list= / ? x / ? y / if (= (list-length / x) (list-length / y)) (if (> (list-length / x) 0) (and (equal (head / x) (head / y)) (list= (tail / x) (tail / y))) (true)) (false);

= (list-length / (list 0)) 0;

= (list-length / (list 4) 6 1 0 4) 4;

= (list-length / (list 6) 6 2 7 0 9 4) 6;

= (list-length / (list 2) 4 9) 2;

= (list-length / (list 3) 6 1 7) 3;

= (head / (list 6) 12 11 10 4 1 5) 12;

list= (tail / (list 6) 12 11 10 4 1 5) ((list 5) 11 10 4 1 5);

= (head / (list 8) 15 13 12 7 10 11 13 18) 15;

list= (tail / (list 8) 15 13 12 7 10 11 13 18) ((list 7) 13 12 7 10 11 13 18);

= (head / (list 2) 11 1) 11;

list= (tail / (list 2) 11 1) ((list 1) 1);

= (head / (list 6) 5 19 4 16 6 11) 5;

list= (tail / (list 6) 5 19 4 16 6 11) ((list 5) 19 4 16 6 11);

= (head / (list 10) 12 18 7 4 9 18 6 16 6 18) 12;

list= (tail / (list 10) 12 18 7 4 9 18 6 16 6 18) ((list 9) 18 7 4 9 18 6 16 6 18);

= (head / (list 6) 19 7 3 10 19 13) 19;

list= (tail / (list 6) 19 7 3 10 19 13) ((list 5) 7 3 10 19 13);

= (head / (list 6) 19 7 19 12 16 13) 19;

list= (tail / (list 6) 19 7 19 12 16 13) ((list 5) 7 19 12 16 13);

= (head / (list 1) 3) 3;

list= (tail / (list 1) 3) ((list 0));

= (head / (list 3) 2 19 17) 2;

list= (tail / (list 3) 2 19 17) ((list 2) 19 17);

= (head / (list 7) 1 16 5 14 6 19 2) 1;

list= (tail / (list 7) 1 16 5 14 6 19 2) ((list 6) 16 5 14 6 19 2);

= (list-ref ((list 3) 18 14 17) 1) 14;

= (list-ref ((list 3) 8 11 10) 2) 10;

= (list-ref ((list 8) 15 0 4 9 9 2 10 17) 3) 9;

= (list-ref ((list 7) 4 8 8 5 14 5 13) 4) 14;

= (list-ref ((list 4) 1 4 7 18) 2) 7;

= (list-ref ((list 3) 12 2 3) 1) 2;

= (list-ref ((list 6) 12 5 7 15 7 16) 2) 7;

= (list-ref ((list 8) 5 15 7 14 7 1 11 19) 0) 5;

= (list-ref ((list 3) 19 17 8) 2) 8;

= (list-ref ((list 4) 10 10 4 11) 1) 10;

list= ((list 0)) ((list 0));

list= ((list 1) 4) ((list 1) 4);

list= ((list 2) 7 5) ((list 2) 7 5);

list= ((list 3) 15 13 11) ((list 3) 15 13 11);

list= ((list 4) 2 8 0 6) ((list 4) 2 8 0 6);

# this next batch of examples are a bit misleading, should streamline

not / list= ((list 0)) ((list 1) 9);

not / list= ((list 0)) ((list 1) 5);

not / list= ((list 1) 18) ((list 2) 8 18);

not / list= ((list 1) 18) ((list 2) 18 5);

not / list= ((list 2) 11 18) ((list 3) 7 11 18);

not / list= ((list 2) 11 18) ((list 3) 11 18 6);

not / list= ((list 3) 7 19 17) ((list 4) 6 7 19 17);

not / list= ((list 3) 7 19 17) ((list 4) 7 19 17 0);

not / list= ((list 4) 10 0 11 1) ((list 5) 0 10 0 11 1);

not / list= ((list 4) 10 0 11 1) ((list 5) 10 0 11 1 8);

# some helpful functions

list= (prepend 8 ((list 0))) ((list 1) 8);

list= (prepend 11 ((list 1) 8)) ((list 2) 11 8);

list= (prepend 13 ((list 2) 1 12)) ((list 3) 13 1 12);

list= (prepend 0 ((list 3) 7 7 5)) ((list 4) 0 7 7 5);

list= (prepend 16 ((list 4) 16 0 19 3)) ((list 5) 16 16 0 19 3);

list= (prepend 10 ((list 5) 5 6 7 9 10)) ((list 6) 10 5 6 7 9 10);

list= (prepend 19 ((list 6) 3 19 18 6 10 16)) ((list 7) 19 3 19 18 6 10 16);

list= (prepend 19 ((list 7) 17 17 10 1 18 12 14)) ((list 8) 19 17 17 10 1 18 12 14);

define pair / ? x / ? y / (list 2) (x) (y);

define first / ? lst / head / lst;

define second / ? lst / head / tail / lst;

list= (pair 3 6) ((list 2) 3 6);

= (first / pair 3 6) 3;

= (second / pair 3 6) 6;

list= (pair 4 9) ((list 2) 4 9);

= (first / pair 4 9) 4;

= (second / pair 4 9) 9;

list= (pair 8 3) ((list 2) 8 3);

= (first / pair 8 3) 8;

= (second / pair 8 3) 3;

define list-find-helper / ? lst / ? key / ? fail / ? idx / if (= (list-length / lst) 0) (fail 0) (if (equal (head / lst) (key)) (idx) (list-find-helper (tail / lst) (key) (fail) (+ (idx) 1)));

define list-find / ? lst / ? key / ? fail / list-find-helper (lst) (key) (fail) 0;

define example-fail / ? x 100;

= (list-find ((list 1) 13) 13 (example-fail)) 0;

= (list-find ((list 10) 0 9 8 16 15 14 17 5 9 2) 15 (example-fail)) 4;

= (list-find ((list 3) 7 4 10) 7 (example-fail)) 0;

= (list-find ((list 6) 0 17 10 13 11 5) 17 (example-fail)) 1;

= (list-find ((list 3) 12 9 6) 12 (example-fail)) 0;

= (list-find ((list 7) 17 1 4 17 14 13 13) 14 (example-fail)) 4;

= (list-find ((list 3) 2 15 2) 15 (example-fail)) 1;

= (list-find ((list 9) 6 13 10 8 10 9 6 15 18) 13 (example-fail)) 1;

= (list-find ((list 3) 12 16 0) 12 (example-fail)) 0;

= (list-find ((list 1) 15) 15 (example-fail)) 0;

= (list-find ((list 4) 2 17 11 5) 14 (example-fail)) 100;

= (list-find ((list 6) 12 1 19 6 17 9) 2 (example-fail)) 100;

= (list-find ((list 8) 11 6 17 8 13 10 9 16) 19 (example-fail)) 100;

17. describe changes to the implicit interpreter to allow new special forms

define base-translate / translate;

define translate / ? x / if (= (x) 32) 64 (base-translate / x);

= 32 64;

= (+ 32 64) 128;

define translate / base-translate;

not / = 32 64;

= (+ 32 64) 96;

# now can create a special form for lists

define translate / ? x / if (number? / x) (base-translate / x) (if (= (head / x) vector) (translate / prepend ((list 2) list (list-length / tail / x)) (tail / x)) (base-translate / x));

list= (vector 1 2 3) ((list 3) 1 2 3);

# now to desugar let expressions

define translate-with-vector / translate;

define translate-let-form / ? x / ? body / if (= (list-length / x) 0) (translate / body) (translate-let-form (tail / x) (vector (vector ? (head / head / x) (body)) (head / tail / head / x)));

define translate / ? x / if (number? / x) (translate-with-vector / x) (if (= (head / x) let) (translate-let-form (head / tail / x) (head / tail / tail / x)) (translate-with-vector / x));

let ((x 20)) (= (x) 20);

let ((x 50) (y 20)) (= (- (x) (y)) 30);

# the is-list function is now on dubious ground
# this stuff will be replaced with typing ASAP

define is-list / ? x / not / number? / x;

is-list / (list 2) 1 3;

is-list / (list 0);

not / is-list 23;

is-list / (list 3) ((list 2) 2 3) 1 (? x / + (x) 10);

18. introduce sugar for let

# if would be good to introduce desugarings more rigorously, but for now...
# ... just a very vague sketch

intro let;

= (let ((x 10)) (+ (x) 5)) ((? x / + (x) 5) 10);

= (let ((x 10) (y 5)) (+ (x) (y))) (((? x / ? y / + (x) (y)) 10) 5);

19. build up functions of several variables

= ((? x / ? y / - (x) (y)) 4 0) 4;

= ((? x / ? y / - (x) (y)) 11 8) 3;

= ((? x / ? y / - (x) (y)) 5 5) 0;

= ((? x / ? y / - (x) (y)) 10 1) 9;

= ((? x / ? y / - (x) (y)) 10 7) 3;

define last / ? x / list-ref (x) (- (list-length / x) 1);

define except-last / ? x / if (> (list-length / x) 1) (prepend (head / x) (except-last / tail / x)) (vector);

# test last and except-last

= 15 (last / vector 4 5 15);

list= (vector 4 5) (except-last / vector 4 5 15);

intro lambda;

define prev-translate / translate;

define translate / let ((prev (prev-translate))) (? x / if (number? / x) (prev / x) (if (= (head / x) lambda) (let ((formals (head / tail / x)) (body (head / tail / tail / x))) (if (> (list-length / formals) 0) (translate (vector lambda (except-last / formals) (vector ? (last / formals) (body)))) (translate (body)))) (prev / x)));

# test lambda

= ((lambda (x y) (- (x) (y))) 8 3) 5;

= ((lambda (x y) (- (x) (y))) 1 1) 0;

= ((lambda (x y) (- (x) (y))) 10 9) 1;

= ((lambda (x y) (- (x) (y))) 7 5) 2;

= ((lambda (x y) (- (x) (y))) 9 8) 1;

define apply / lambda (x y) (if (list= (y) (vector)) (x) (apply ((x) (head / y)) (tail / y)));

= (apply (lambda (x y) (- (x) (y))) (vector 8 6)) 2;

= (apply (lambda (x y) (- (x) (y))) (vector 5 0)) 5;

= (apply (lambda (x y) (- (x) (y))) (vector 12 9)) 3;

= (apply (lambda (x y) (- (x) (y))) (vector 13 8)) 5;

= (apply (lambda (x y) (- (x) (y))) (vector 11 3)) 8;

20. show map function for applying a function across the elements of a list

define map / lambda (p lst) (if (> (list-length / lst) 0) (prepend (p (head / lst)) (map (p) (tail / lst))) (vector));

list= (map (? x / * (x) 2) (vector 0 8 15)) (vector 0 16 30);

list= (map (? x / * (x) 2) (vector 12 4 0 9)) (vector 24 8 0 18);

list= (map (? x / * (x) 2) (vector 8 9 5 7 10)) (vector 16 18 10 14 20);

list= (map (? x / * (x) 2) (vector 10 12 19 8 3 1)) (vector 20 24 38 16 6 2);

list= (map (? x 42) (vector 5 18 4)) (vector 42 42 42);

list= (map (? x 42) (vector 3 10 17 11)) (vector 42 42 42 42);

list= (map (? x 42) (vector 5 13 6 16 2)) (vector 42 42 42 42 42);

list= (map (? x 42) (vector 9 1 19 14 6 10)) (vector 42 42 42 42 42 42);

define crunch / lambda (p lst) (if (>= (list-length / lst) 2) (p (head / lst) (crunch (p) (tail / lst))) (if (= (list-length / lst) 1) (head / lst) (undefined)));

= (crunch (+) (vector 5 12 2)) 19;

= (crunch (+) (vector 11 18 1 4)) 34;

= (crunch (+) (vector 15 13 10 12 2)) 52;

= (crunch (+) (vector 12 6 17 15 4 10)) 64;

21. end of part 1, start of part 2

# The following parts of the message are experimental, and not
# carefully integrated with the main body

intro part2;

22. show an example of recursive evaluation

# skipping over a lot of definitions and desugarings

define easy-factorial / ? f / ? x / if (> (x) 0) (* (x) / f (f) (- (x) 1)) 1;

define factorial / ? x / if (> (x) 0) (* (x) / factorial / - (x) 1) 1;

= (easy-factorial (easy-factorial) 0) 1;

= (easy-factorial (easy-factorial) 1) 1;

= (easy-factorial (easy-factorial) 2) 2;

= (easy-factorial (easy-factorial) 3) 6;

= (easy-factorial (easy-factorial) 4) 24;

= (easy-factorial (easy-factorial) 5) 120;

= (factorial 0) 1;

= (factorial 1) 1;

= (factorial 2) 2;

= (factorial 3) 6;

= (factorial 4) 24;

= (factorial 5) 120;

23. some pure lambda calculus definitions - optional

# these definitions are not quite what we want
# since thinking of everything as a function requires headscratching
# it would be better to use these as a parallel means of evaluation
# ... for expressions

define pure-if / ? x / ? y / ? z / x (y) (z);

define pure-true / ? y / ? z / y;

define pure-false / ? y / ? z / z;

define pure-cons / ? x / ? y / ? z / pure-if (z) (x) (y);

define pure-car / ? x / x (pure-true);

define pure-cdr / ? x / x (pure-false);

define zero / ? f / ? x / x;

define one / ? f / ? x / f (x);

define two / ? f / ? x / f (f (x));

define succ / ? n / ? f / ? x / f ((n (f)) (x));

define add / ? a / ? b / (a (succ)) (b);

define mult / ? a / ? b / (a (add / b)) (zero);

define pred / ? n / pure-cdr / (n (? p / pure-cons (succ / pure-car / p) (pure-car / p))) (pure-cons (zero) (zero));

define is-zero / ? n / (n (? dummy / pure-false) (pure-true));

define fixed-point / ? f / (? x / f (x (x))) (? x / f (x (x)));

# .. but for rest of message will assume that define does fixed-point for us
# now build a link between numbers and church number functions

define unchurch / ? c / c (? x / + (x) 1) 0;

= 0 (unchurch / zero);

= 1 (unchurch / one);

= 2 (unchurch / two);

define church / ? x / if (= 0 (x)) (zero) (succ / church / - (x) 1);

24. introduce universal quantifier

# really need to link with sets for true correctness
# and the examples here are REALLY sparse, need much more

intro forall;

< 5 (+ 5 1);

< 4 (+ 4 1);

< 3 (+ 3 1);

< 2 (+ 2 1);

< 1 (+ 1 1);

< 0 (+ 0 1);

forall (? x / < (x) (+ (x) 1));

< 5 (* 5 2);

< 4 (* 4 2);

< 3 (* 3 2);

< 2 (* 2 2);

< 1 (* 1 2);

not / < 0 (* 0 2);

not / forall (? x / < (x) (* (x) 2));

25. introduce existential quantifier

# really need to link with sets for true correctness
# and the examples here are REALLY sparse, need much more

not / = 5 (* 2 2);

= 4 (* 2 2);

not / = 3 (* 2 2);

not / = 2 (* 2 2);

not / = 1 (* 2 2);

not / = 0 (* 2 2);

intro exists;

exists (? x / = (x) (* 2 2));

not / = 5 (+ 5 2);

not / = 4 (+ 4 2);

not / = 3 (+ 3 2);

not / = 2 (+ 2 2);

not / = 1 (+ 1 2);

not / = 0 (+ 0 2);

not (exists (? x / = (x) (+ (x) 2)));

26. introduce logical implication

intro =>;

define => / ? x / ? y / not / and (x) (not / y);

=> (true) (true);

not / => (true) (false);

=> (false) (true);

=> (false) (false);

forall (? x / forall (? y / => (=> (x) (y)) (=> (not / y) (not / x))));

27. introduce sets and set membership

intro element;

define element / ? x / ? lst / not / = (list-find-helper (lst) (x) (? y 0) 1) 0;

element 0 (vector 0 4 8 3 5);

element 5 (vector 0 4 8 3 5);

element 3 (vector 0 4 8 3 5);

element 3 (vector 3 5 1 0 9);

element 1 (vector 3 5 1 0 9);

element 5 (vector 3 5 1 0 9);

element 5 (vector 8 1 6 2 0 5);

element 6 (vector 8 1 6 2 0 5);

element 5 (vector 8 1 6 2 0 5);

element 5 (vector 5 3 8 6 2 9);

element 5 (vector 5 3 8 6 2 9);

element 9 (vector 5 3 8 6 2 9);

element 7 (vector 1 7 2 6 4 5);

element 2 (vector 1 7 2 6 4 5);

element 6 (vector 1 7 2 6 4 5);

not / element 7 (vector 8 3 9 6);

not / element 1 (vector 8 6 3 5 4);

not / element 2 (vector 9 5 6);

not / element 5 (vector 2 0 7);

not / element 6 (vector 3 5);

# rules for set equality

define set-subset / ? x / ? y / if (> (list-length / x) 0) (and (element (head / x) (y)) (set-subset (tail / x) (y))) (true);

define set= / ? x / ? y / and (set-subset (x) (y)) (set-subset (y) (x));

set= (vector 1 5 9) (vector 5 1 9);

set= (vector 1 5 9) (vector 9 1 5);

not / set= (vector 1 5 9) (vector 1 5);

# let's go leave ourselves wide open to Russell's paradox
# ... by using characteristic functions
# ... since it doesn't really matter for communication purposes
# ... and so far this is just used/tested with sets of integers really

element 5 (all (? x / = (+ (x) 10) 15));

element 3 (all (? x / = (* (x) 3) (+ (x) 6)));

define empty-set / vector;

element 0 (natural-set);

forall (? x / => (element (x) (natural-set)) (element (+ (x) 1) (natural-set)));

element 1 (natural-set);

element 2 (natural-set);

element 3 (natural-set);

element 4 (natural-set);

element 5 (natural-set);

element 6 (natural-set);

element 7 (natural-set);

element 8 (natural-set);

element 9 (natural-set);

define boolean-set / vector (true) (false);

element (true) (boolean-set);

element (false) (boolean-set);

# actually, to simplify semantics elsewhere, true and false
# are now just 0 and 1 so they are not distinct from ints

define even-natural-set / all / ? x / exists / ? y / and (element (y) (natural-set)) (= (* 2 (y)) (x));

element 0 (natural-set);

element 0 (even-natural-set);

element 1 (natural-set);

not / element 1 (even-natural-set);

element 2 (natural-set);

element 2 (even-natural-set);

element 3 (natural-set);

not / element 3 (even-natural-set);

element 4 (natural-set);

element 4 (even-natural-set);

element 5 (natural-set);

not / element 5 (even-natural-set);

element 6 (natural-set);

element 6 (even-natural-set);

28. introduce graph structures

define make-graph / lambda (nodes links) (pair (nodes) (links));

define test-graph / make-graph (vector 1 2 3 4) (vector (vector 1 2) (vector 2 3) (vector 1 4));

define graph-linked / lambda (g n1 n2) (exists / ? idx / if (and (>= (idx) 0) (< (idx) (list-length / list-ref (g) 1))) (list= (list-ref (list-ref (g) 1) (idx)) (vector (n1) (n2))) (false));

= (graph-linked (test-graph) 1 2) (true);

= (graph-linked (test-graph) 1 3) (false);

= (graph-linked (test-graph) 2 4) (false);

# 'if' is used a lot in the next definition in place of and/or
# this is because I haven't established lazy evaluation forms for and/or
# so this very inefficient algorithm completely bogs down when combined
# ... during testing with a dumb implementation for 'exists'.

define graph-linked* / lambda (g n1 n2) (if (= (n1) (n2)) (true) (if (graph-linked (g) (n1) (n2)) (true) (exists (? n3 / if (graph-linked (g) (n1) (n3)) (graph-linked* (g) (n3) (n2)) (false)))));

= (graph-linked* (test-graph) 1 2) (true);

= (graph-linked* (test-graph) 1 3) (true);

= (graph-linked* (test-graph) 2 4) (false);

29. show how to execute a sequence of instructions

intro begin;

define prev-translate / translate;

define reverse / ? x / if (>= (list-length / x) 1) (prepend (last / x) (reverse / except-last / x)) (x);

# test reverse

list= (vector 1 2 3) (reverse / vector 3 2 1);

define translate / let ((prev (prev-translate))) (? x / if (number? / x) (prev / x) (if (= (head / x) begin) (translate (vector (vector ? x (vector last (vector x))) (prepend vector (tail / x)))) (prev / x)));

= (begin 1 7 2 4) 4;

= (begin (set! (demo-mut1) 88) (set! (demo-mut1) 6) (get! / demo-mut1)) 6;

= (begin (set! (demo-mut2) 88) (set! (demo-mut1) 6) (get! / demo-mut2)) 88;

= (begin (set! (demo-mut1) 88) (set! (demo-mut1) 6) (get! / demo-mut1) 4) 4;

30. introduce environment/hashmap structure

# this section needs a LOT more examples :-)
# note that at the time of writing (h 1 2) is same as ((h) 1 2)

define hash-add / lambda (h x y z) (if (equal (z) (x)) (y) (h (z)));

define hash-ref / lambda (h x) (h (x));

define hash-null / ? x / undefined;

define hash-default / ? default / ? x / default;

define test-hash / hash-add (hash-add (hash-null) 3 2) 4 9;

= (hash-ref (test-hash) 4) 9;

= (hash-ref (test-hash) 3) 2;

= (hash-ref (test-hash) 8) (undefined);

= (hash-ref (test-hash) 15) (undefined);

= (hash-ref (hash-add (test-hash) 15 33) 15) 33;

= (hash-ref (test-hash) 15) (undefined);

define make-hash / ? x / if (list= (x) (vector)) (hash-null) (hash-add (make-hash (tail / x)) (first / head / x) (second / head / x));

= (hash-ref (make-hash / vector (pair 3 10) (pair 2 20) (pair 1 30)) 3) 10;

= (hash-ref (make-hash / vector (pair 3 10) (pair 2 20) (pair 1 30)) 1) 30;

31. introduce simple mutable structures

define mutable-struct / ? lst / let ((data (map (? x / make-cell 0) (lst)))) (? key / list-ref (data) (list-find (lst) (key) (? x 0)));

define test-struct1 / mutable-struct / vector item1 item2 item3;

set! (test-struct1 item1) 15;

= (get! / test-struct1 item1) 15;

32. introduce method handler wrappers

define add-method / lambda (object name method) (hash-add (object) (name) (? dummy / method / object));

define call / ? x / x 0;

define test-struct2 / mutable-struct / vector x y;

set! (test-struct2 x) 10;

set! (test-struct2 y) 20;

= (get! / test-struct2 x) 10;

= (get! / test-struct2 y) 20;

define test-struct3 / add-method (test-struct2) sum (? self / + (get! / self x) (get! / self y));

= (get! / test-struct3 x) 10;

= (get! / test-struct3 y) 20;

= (call / test-struct3 sum) 30;

set! (test-struct3 y) 10;

= (call / test-struct3 sum) 20;

set! (test-struct2 y) 5;

= (call / test-struct3 sum) 15;

33. introduce turing machine model

# just for fun!

define safe-tail / ? x / if (> (list-length / x) 0) (if (> (list-length / x) 1) (tail / x) (vector / vector)) (vector / vector);

define safe-head / ? x / if (> (list-length / x) 0) (head / x) (vector);

define tape-read / ? tape / let ((x (second / tape))) (if (> (list-length / x) 0) (head / x) (vector));

define tape-transition / lambda (tape shift value) (if (= (shift) 1) (pair (prepend (value) (first / tape)) (safe-tail / second / tape)) (if (= (shift) 0) (pair (safe-tail / first / tape) (prepend (safe-head / first / tape) (prepend (value) (safe-tail / second / tape)))) (pair (first / tape) (prepend (value) (safe-tail / second / tape)))));

define turing / lambda (machine current last tape) (if (= (current) (last)) (tape) (let ((next (machine (current) (tape-read / tape)))) (turing (machine) (list-ref (next) 0) (last) (tape-transition (tape) (list-ref (next) 1) (list-ref (next) 2)))));

define make-tape / ? x / pair (vector) (x);

define remove-trail / ? x / ? lst / if (> (list-length / lst) 0) (if (equal (last / lst) (x)) (remove-trail (x) (except-last / lst)) (lst)) (lst);

define extract-tape / ? x / remove-trail (vector) (second / x);

define tm-binary-increment / make-hash / vector (pair right (make-hash / vector (pair 0 (vector right 1 0)) (pair 1 (vector right 1 1)) (pair (vector) (vector inc 0 (vector))))) (pair inc (make-hash / vector (pair 0 (vector noinc 0 1)) (pair 1 (vector inc 0 0)) (pair (vector) (vector halt 2 1)))) (pair noinc (make-hash / vector (pair 0 (vector noinc 0 0)) (pair 1 (vector noinc 0 1)) (pair (vector) (vector halt 1 (vector))))) (pair halt (make-hash / vector));

list= (extract-tape / turing (tm-binary-increment) right halt (make-tape / vector 1 0 0 1)) (vector 1 0 1 0);

list= (extract-tape / turing (tm-binary-increment) right halt (make-tape / vector 1 1 1)) (vector 1 0 0 0);

list= (extract-tape / turing (tm-binary-increment) right halt (make-tape / vector 1 1 1 0 0 0 1 1 1)) (vector 1 1 1 0 0 1 0 0 0);

34. introduce simple form of typing, for ease of documentation.

# An object is simply a function that takes an argument.
# The argument is the method to call on the object.
# Types are here taken to be just the existence of a particular method,
# with that method returning an object of the appropriate type.

define make-integer
  (lambda (v)
    (lambda (x)
      (if (= (x) int)
      (v)
      0)));

define objectify
  (? x 
     (if (number? (x))
     (make-integer (x))
     (x)));

define instanceof
  (lambda (T t)
    (if (number? (t))
    (= (T) int)
    (not (number? ((objectify (t)) (T))))));

# add version of lambda that allows types to be declared

define prev-translate (translate);

define translate
  (let ((prev (prev-translate)))
    (? x
      (if (number? (x))
        (prev (x))
        (if (= (head (x)) lambda)
          (let ((formals (head (tail (x))))
                (body (head (tail (tail (x))))))
            (if (> (list-length (formals)) 0)
        (if (number? (last (formals)))
            (translate
             (vector
              lambda
              (except-last (formals))
              (vector ? (last (formals)) (body))))
            (let ((formal-name (first (last (formals))))
              (formal-type (second (last (formals)))))
              (translate
               (vector
            lambda
            (except-last (formals))
            (vector 
             ? 
             (formal-name) 
             (vector 
              let
              (vector (vector 
                   (formal-name) 
                   (vector
                    (vector objectify (vector (formal-name)))
                    (formal-type))))
              (body)))))))
        (translate (body))))
          (prev (x))))));

# add conditional form

define prev-translate (translate);

define translate
  (let ((prev (prev-translate)))
    (? x
      (if (number? (x))
        (prev (x))
        (if (= (head (x)) cond)
          (let ((cnd (head (tail (x))))
                (rem (tail (tail (x)))))
            (if (> (list-length (rem)) 0)
        (translate
         (vector
                  if
          (first (cnd))
          (second (cnd))
          (prepend cond (rem))))
        (translate (cnd))))
          (prev (x))))));

= 99 (cond 99);

= 8 (cond ((true) 8) 11);

= 11 (cond ((false) 8) 11);

= 7 (cond ((false) 3) ((true) 7) 11);

= 3 (cond ((true) 3) ((true) 7) 11);

= 11 (cond ((false) 3) ((false) 7) 11);

define remove-match 
  (lambda (test lst)
    (if (> (list-length (lst)) 0)
    (if (test (head (lst)))
        (remove-match (test) (tail (lst)))
        (prepend (head (lst)) (remove-match (test) (tail (lst)))))
    (lst)));

define remove-element
  (lambda (x) 
    (remove-match (lambda (y) (= (y) (x)))));

list= (vector 1 2 3 5) (remove-element 4 (vector 1 2 3 4 5));

list= (vector 1 2 3 5) (remove-element 4 (vector 1 4 2 4 3 4 5));

define return
  (lambda (T t)
    (let ((obj (objectify (t))))
      (obj (T))));

define tester
  (lambda ((x int) (y int))
    (return int (+ (x) (y))));

= 42 (tester (make-integer 10) (make-integer 32));

= 42 (tester 10 32);

define reflective
  (lambda (f)
    ((lambda (x)
       (f (lambda (y) ((x (x)) (y)))))
     (lambda (x)
       (f (lambda (y) ((x (x)) (y)))))));

35. an example object -- a 2D point

define point
  (lambda (x y)
    (reflective
     (lambda (self msg)
       (cond ((= (msg) x) (x))
         ((= (msg) y) (y))
         ((= (msg) point) (self))
         ((= (msg) +) 
          (lambda ((p point))
        (point (+ (x) (p x))
               (+ (y) (p y)))))
         ((= (msg) =) 
          (lambda ((p point))
        (and (= (x) (p x))
             (= (y) (p y)))))
         0))));

define point1 (point 1 11);

define point2 (point 2 22);

= 1 (point1 x);

= 22 (point2 y);

= 11 ((point 11 12) x);

= 11 (((point 11 12) point) x);

= 16 (((point 16 17) point) x);

= 33 (point1 + (point2) y);

point1 + (point2) = (point 3 33);

point2 + (point1) = (point 3 33);

(point 100 200) + (point 200 100) = (point 300 300);

instanceof point (point1);

not (instanceof int (point1));

instanceof int 5;

not (instanceof point 5);

36. an example object -- a container

define container
  (lambda (x)
    (let ((contents (make-cell (vector))))
      (reflective
       (lambda (self msg)
     (cond ((= (msg) container) (self))
           ((= (msg) inventory) (get! (contents)))
           ((= (msg) add)
        (lambda (x) 
          (if (not (element (x) (get! (contents))))
              (set! (contents) (prepend (x) (get! (contents))))
              (false))))
           ((= (msg) remove)
        (lambda (x)
          (set! (contents) (remove-element (x) (get! (contents))))))
           ((= (msg) =)
        (lambda ((c container))
          (set= (self inventory) (c inventory))))
           0)))));

# Can pass anything to container function to create an object
# Should eventually use a consistent protocol for all objects,
# but all this stuff is still in flux

define pocket (container new);

pocket add 77;

pocket add 88;

pocket add 99;

set= (pocket inventory) (vector 77 88 99);

pocket remove 88;

set= (pocket inventory) (vector 77 99);

define pocket2 (container new);

pocket2 add 77;

pocket2 add 99;

pocket2 = (pocket);

37. expressing inheritance

# counter-container adds one method to container: count

define counter-container
  (lambda (x)
    (let ((super (container new)))
      (reflective
       (lambda (self msg)
     (cond ((= (msg) counter-container) (self))
           ((= (msg) count) (list-length (super inventory)))
           (super (msg)))))));

define cc1 (counter-container new);

= 0 (cc1 count);

cc1 add 4;

= 1 (cc1 count);

cc1 add 5;

= 2 (cc1 count);

38. adding a special form for classes

# need a bunch of extra machinery first, will push this
# back into previous sections eventually, and simplify

define list-append
  (lambda (lst1 lst2)
    (if (> (list-length (lst1)) 0)
    (list-append (except-last (lst1))
             (prepend (last (lst1)) (lst2)))
    (lst2)));

list= (list-append (vector 1 2 3) (vector 4 5 6)) (vector 1 2 3 4 5 6);

define append
  (? x
     (? lst
    (if (> (list-length (lst)) 0)
        (prepend (head (lst)) (append (x) (tail (lst))))
        (vector (x)))));

list= (append 5 (vector 1 2)) (vector 1 2 5);

define select-match 
  (lambda (test lst)
    (if (> (list-length (lst)) 0)
    (if (test (head (lst)))
        (prepend (head (lst)) (select-match (test) (tail (lst))))
        (select-match (test) (tail (lst))))
    (lst)));

define unique
  (let ((store (make-cell 0)))
    (lambda (x)
      (let ((id (get! (store))))
    (begin
      (set! (store) (+ (id) 1))
      (id)))));

= (unique new) 0;

= (unique new) 1;

= (unique new) 2;

not (= (unique new) (unique new));

define setup-this
  (lambda (this self)
    (if (number? / this)
    (self)
    (this)));

# okay, here it comes.  don't panic!
# I need to split this up into helpers, and simplify.
# It basically just writes code for classes like we saw in
# a previous section.

define prev-translate (translate);

define translate
  (let ((prev (prev-translate)))
    (? x
       (if (number? (x))
       (prev (x))
       (if (= (head (x)) class)
           (let ((name (list-ref (x) 1))
             (args (list-ref (x) 2))
             (fields (tail (tail (tail (x))))))
         (translate
          (vector
           define
           (name)
           (vector
            lambda
            (prepend ext-this (args))
            (vector
             let
             (append
              (vector unique-id (vector unique new))
              (map 
               (tail)
               (select-match (? x (= (first (x)) field)) (fields))))
             (vector
              let
              (vector
               (vector
            self
            (vector
             reflective
             (vector
              lambda
              (vector self)
              (vector
               let
               (vector 
                (vector
                 this
                 (vector setup-this 
                     (vector ext-this)
                     (vector self))))
               (vector 
                let
                (vector (vector ignore-this 1))
                (vector
                 lambda
                 (vector method)
                 (list-append
                  (prepend
                   cond
                   (list-append
                (map
                 (? x 
                    (vector
                     (vector = (vector method) (first (x)))
                     (second (x))))
                 (map (tail)
                      (select-match 
                       (? x (= (first (x)) method)) 
                       (fields))))
                (map
                 (? x 
                    (vector
                     (vector = (vector method) (x))
                     (vector (x))))
                 (map (second)
                      (select-match 
                       (? x (= (first (x)) field)) 
                       (fields))))))
                  (vector
                   (vector
                (vector = (vector method) self)
                (vector self))
                   (vector
                (vector = (vector method) (name))
                (vector self self))
                   (vector
                (vector = (vector method) classname)
                (name))
                   (vector
                (vector = (vector method) unknown)
                (vector lambda (vector x) 0))
                   (vector
                (vector = (vector method) new)
                0)
                   (vector
                (vector = (vector method) unique-id)
                (vector unique-id))
                   (vector
                (vector = (vector method) ==)
                (vector
                 lambda
                 (vector x)
                 (vector = 
                     (vector unique-id)
                     (vector x unique-id))))
                   (vector self unknown (vector method)))))))))))
              (vector 
               begin
               (vector self new)
               (vector self))))))))
           (prev (x))))));

# revisit the point class example

class point (x y) 
       (method x (x))
       (method y (y))
       (method + (lambda ((p point))
           (point new 
              (+ (x) (p x))
              (+ (y) (p y)))))
       (method = (lambda ((p point))
           (and (= (x) (p x))
            (= (y) (p y)))));

# note the appearance of new in the next line --
# this is the only difference to previous version

define point1 (point new 1 11);

define point2 (point new 2 22);

= 1 (point1 x);

= 22 (point2 y);

= 11 ((point new 11 12) x);

= 11 (((point new 11 12) point) x);

= 16 (((point new 16 17) point) x);

= 33 (point1 + (point2) y);

point1 + (point2) = (point new 3 33);

point2 + (point1) = (point new 3 33);

(point new 100 200) + (point new 200 100) = (point new 300 300);

instanceof point (point1);

not (instanceof int (point1));

# Check that virtual calls can be made to work.
# They are a little awkward right now.
# Should they be the default?

class c1 ()
       (method getid 100)
       (method altid (this getid));

class c2 ()
       (field super-ref (make-cell 0))
       (method new (set! (super-ref) (c1 / this)))
       (method super (? x ((get! / super-ref) (x))))
       (method unknown (? x (self super / x)))
       (method getid 200);

= 100 / c1 new altid;

= 200 / c2 new altid;

39. wrapper class for cells

class cell (initial-value)
       (field content (make-cell (initial-value)))
       (method get (get! (content)))
       (method set (lambda (new-value)
             (set! (content) (new-value))))
       (method reset (self set (initial-value)))
       (method unknown (lambda (x) ((objectify (self get)) (x))));

define cell-test1 (cell new 15);

= 15 (cell-test1 get);

cell-test1 set 82;

= 82 (cell-test1 get);

define cell-test2 (cell new (point new 120 150));

define cell-test3 (cell new (point new 300 300));

cell-test2 + (cell-test3) = (point new 420 450);

not (cell-test2 = (cell-test3));

cell-test3 set (cell-test2);

cell-test2 = (cell-test3);

40. playing around with doors and rooms

class door ((src room) (dest room))
       (method new (begin
             (src add (self))
             (dest add (self))))
       (method access-from (lambda ((current room))
                 (cond ((current == (src)) (dest))
                   ((current == (dest)) (src))
                   0)))
       (method is-present (lambda ((current room))
                (cond ((current == (src)) (true))
                  ((current == (dest)) (true))
                  (false))));

class room (name)
       (field content (container new))
       (method name (name))
       (method unknown (lambda (x) (content (x))));

# need to fix up containers to use object equality

define object-element
  (lambda (n lst)
    (> (list-length 
    (select-match (lambda (x) (x == (n))) (lst))) 
       0));

class container ()
    (field contents (cell new (vector)))
    (method inventory (contents get))
    (method add (lambda (x) 
          (if (not (object-element (x) (contents get)))
              (contents set (prepend (x) (contents get)))
              (false))));

define hall (room new 0);

define kitchen (room new 1);

define door1 (door new (hall) (kitchen));

(first (hall inventory)) == (door1);

(first (kitchen inventory)) == (door1);

door1 access-from (hall) == (kitchen);

not (door1 access-from (hall) == (hall));

door1 access-from (kitchen) == (hall);

define stairs (room new 2);

define lawn (room new 3);

define bedroom (room new 4);

define nowhere (room new 0);

define door2 (door new (hall) (lawn));

define door3 (door new (hall) (stairs));

define door4 (door new (stairs) (bedroom));

class character ()
       (field location (cell new 0))
       (field name (cell new 0))
       (method set-room (lambda ((r room)) 
              (begin
                (if (not (number? / location get))
                (location get remove (self))
                0)
                (r add (self))
                (location set (r)))))
       (method get-room (location get))
       (method set-name (lambda (n) (name set / n)))
       (method get-name (name get))
       (method update 0);

define find-max-helper
  (lambda (test max idx n lst)
    (if (> (list-length (lst)) 0)
    (if (> (test (head (lst))) (max))
        (find-max-helper (test) (test (head (lst))) (n) (+ (n) 1) (tail (lst)))
        (find-max-helper (test) (max) (idx) (+ (n) 1) (tail (lst))))
    (idx)));

define find-max-idx
  (lambda (test lst)
    (find-max-helper (test) (test (head (lst))) 0 0 (lst)));

define find-min-helper
  (lambda (test max idx n lst)
    (if (> (list-length (lst)) 0)
    (if (< (test (head (lst))) (max))
        (find-min-helper (test) (test (head (lst))) (n) (+ (n) 1) (tail (lst)))
        (find-min-helper (test) (max) (idx) (+ (n) 1) (tail (lst))))
    (idx)));

define find-min-idx
  (lambda (test lst)
    (find-min-helper (test) (test (head (lst))) 0 0 (lst)));

= 2 (find-max-idx (lambda (x) (x)) (vector 3 4 5 0));

= 1 (find-max-idx (lambda (x) (x)) (vector 3 5 4 0));

= 0 (find-max-idx (lambda (x) (x)) (vector 5 3 4 0));

# the robo class makes a character that patrols from room to room

class robo ()
       (field super (character new))
       (field timestamp (cell new 1))
       (field timestamp-map (cell new (lambda (x) 0)))
       (method unknown (lambda (x) (super (x))))
       (method update 
           (let ((exits 
              (select-match (lambda (x) (instanceof door (x)))
                    (self location inventory))))
         (let ((timestamps
            (map (lambda (x) (timestamp-map get (x)))
                 (exits))))
           (let ((chosen-exit (list-ref 
                       (exits)
                       (find-min-idx (lambda (x) (x))
                             (timestamps))))
             (current-tmap (timestamp-map get))
             (current-t (timestamp get)))
             (begin
               (self location set (chosen-exit 
                       access-from 
                       (self location get)))
               (timestamp-map set 
                      (lambda ((d door))
                    (if (d == (chosen-exit))
                        (current-t)
                        (current-tmap (d)))))
               (timestamp set (+ (timestamp get) 1)))))));

define myrobo (robo new);

myrobo set-room (stairs);

define which-room
  (lambda ((rr robo))
    (find-max-idx 
     (lambda ((r room)) (if (r == (rr get-room)) 1 0))
     (vector (hall) (kitchen) (stairs) (lawn) (bedroom))));

define sequencer
  (lambda (n current lst)
    (if (< (current) (n))
    (begin
      (myrobo update)
      (sequencer
       (n)
       (+ (current) 1)
       (append
        (which-room (myrobo))
        (lst))))
    (lst)));

# here is a list of the first 30 rooms the robot character visits
# 0=hall, 1=kitchen, 2=stairs, 3=lawn, 4=bedroom

list= (sequencer 30 0 (vector)) (vector 4 2 0 3 0 1 0 2 4 2 0 3 0 1 0 2 4 2 0 3 0 1 0 2 4 2 0 3 0 1);

# Now should start to introduce a language to talk about what is
# going on in the simulated world, and start to move away from
# detailed mechanism

41. end of part 2, start of part 3

# The following parts of the message are the beginnings
# of embedding an alternate visual primer

intro part3;

42. simulating unless gates

# for embedded image-and-logic-based primer

# practice with pure logic gate

# X unless Y = (X if Y=0, otherwise 0)

define unless /
  ? x / ? y /
  and (x) (not (y));

# if second input is true, output is blocked (false)
# if second input is false, output copies first input

= (false) (unless (false) (false));

= (true) (unless (true) (false));

= (false) (unless (false) (true));

= (false) (unless (true) (true));

# To do: add a simple simulator for non-grid-based
# logic -- much simpler to understand than
# grid-based

# On to a grid-based logic simulation
# first, need unbounded, mutable matrices

define make-matrix /
  ? default /
  (make-cell (hash-default (default)));

define matrix-set /
  ? m /
  ? x /
  ? addr /
  set! (m) / hash-add (get! (m)) (addr) (x);

define matrix-get /
  ? m /
  ? addr /
  hash-ref (get! (m)) (addr);

define test-matrix
  (make-matrix 0);

= 0 / matrix-get (test-matrix) / vector 1 2 3;

matrix-set (test-matrix) 10 / vector 1 2 3;

= 10 / matrix-get (test-matrix) / vector 1 2 3;

# go through a circuit of unless gates and analyze data flow

define unless-phase-1 /
  ? circuit /
  assign state (make-matrix (false))
  (begin
    (map 
     (? gate /
    assign x1 (list-ref (gate) 0) /
    assign y1 (list-ref (gate) 1) /
    assign x2 (list-ref (gate) 2) /
    assign y2 (list-ref (gate) 3) /
    assign v (list-ref (gate) 4) /
    (if (= (x1) (x2))
        (begin
          (matrix-set (state) (v) / vector (x2) (y2) vert-value)
          (matrix-set (state) (true) / vector (x2) (y2) vert-have)
          (matrix-set (state) (true) / vector (x1) (y1) vert-want)
          (gate))
        (begin
          (matrix-set (state) (v) / vector (x2) (y2) horiz-value)
          (matrix-set (state) (true) / vector (x2) (y2) horiz-have)
          (matrix-set (state) (true) / vector (x1) (y1) horiz-want)
          (gate))))
     (circuit))
    (state));

# move forward one simulation step

define unless-phase-2 /
  ? circuit /
  ? state
  (map 
   (? gate /
      assign x1 (list-ref (gate) 0) /
      assign y1 (list-ref (gate) 1) /
      assign x2 (list-ref (gate) 2) /
      assign y2 (list-ref (gate) 3) /
      assign v (list-ref (gate) 4) /
      assign nv (if (= (x1) (x2))
            (if (matrix-get (state) / vector (x1) (y1) vert-have)
            (and (matrix-get (state) /
                     vector (x1) (y1) vert-value)
                 (not (and (matrix-get (state) /
                           vector (x1) (y1) horiz-value)
                       (not (matrix-get (state) /
                            vector (x1) (y1) horiz-want)))))
            (if (matrix-get (state) / vector (x1) (y1) horiz-have)
                (matrix-get (state) / vector (x1) (y1) horiz-value)
                (true)))
            (if (matrix-get (state) / vector (x1) (y1) horiz-have)
            (and (matrix-get (state) / vector (x1) (y1) horiz-value)
                 (not (and (matrix-get (state) /
                           vector (x1) (y1) vert-value)
                       (not (matrix-get (state) /
                            vector (x1) (y1) vert-want)))))
            (if (matrix-get (state) / vector (x1) (y1) vert-have)
                (matrix-get (state) / vector (x1) (y1) vert-value)
                (true)))) /
                vector (x1) (y1) (x2) (y2) (nv))
   (circuit));

# wrap up both phases of simulation

define simulate-unless /
  ? circuit /
  assign state (unless-phase-1 (circuit)) /
  unless-phase-2 (circuit) (state);

# A circuit is a list of gates
# Each gate is a list (x1 y1 x2 y2 v)
# where the coordinates (x1,y1) and (x2,y2) represent
# start and end points of a wire on a plane, carrying a 
# logic value v.
# Wires copy values from their start point.
#   |  
#   | (A)
#   V        
# -->-->
# (B)(C)
#
# Wire C here copies from wire B.
# If wire A is on, it blocks (sets to 0) C.

assign circuit1
    (vector
     (vector 2 2 4 2 (true))
     (vector 4 2 6 2 (true))
     (vector 6 2 8 2 (true))
     (vector 6 4 6 2 (true))) /
     assign circuit2
     (vector
      (vector 2 2 4 2 (true))
      (vector 4 2 6 2 (true))
      (vector 6 2 8 2 (false))
      (vector 6 4 6 2 (true))) /
      equal (simulate-unless (circuit1)) (circuit2);

# okay, now let us make a simple image class
# we are going to encode each row as a single binary number,
# rather than a vector, so that images will be pretty
# obvious in the raw, uninterpreted message

define bit-get /
  lambda (n offset) /
  assign div2 (div (n) 2) 
  (if (= 0 / offset)
      (not / = (n) / * 2 / div2)
      (bit-get (div2) / - (offset) 1));

= 0 / bit-get (::.) 0;

= 1 / bit-get (::.) 1;

= 1 / bit-get (::.) 2;

= 0 / bit-get (::.) 3;

= 0 / bit-get (::.) 4;

= 0 / bit-get 8 0;

= 0 / bit-get 8 1;

= 0 / bit-get 8 2;

= 1 / bit-get 8 3;

define make-image /
  lambda (h w lst) /
  vector (h) (w) (lst);

define image-get /
  lambda (image row col) /
  assign h (list-ref (image) 0) /
  assign w (list-ref (image) 1) /
  assign lst (list-ref (image) 2) /
  assign bits (list-ref (lst) (row)) /
  bit-get (bits) (- (- (w) (col)) 1);

define image-height /
  ? image /
  list-ref (image) 0;

define image-width /
  ? image /
  list-ref (image) 1;

define test-image /
  make-image 3 5 /
  vector (:....) (:...:) (:....);

= 3 (image-height / test-image);

= 5 (image-width / test-image);

= (true) (image-get (test-image) 0 0);

= (false) (image-get (test-image) 0 1);

= (false) (image-get (test-image) 0 4);

= (true) (image-get (test-image) 1 0);

= (true) (image-get (test-image) 2 0);

= (true) (image-get (test-image) 1 4);

# need a way to join two lists

define merge-list /
  ? lst1 /
  ? lst2 /
  (if (> (list-length / lst1) 0)
      (prepend (head / lst1) (merge-list (tail / lst1) (lst2)))
      (lst2));

define merge-lists /
  ? lst /
  (if (> (list-length / lst) 2)
      (merge-list (head / lst) (merge-lists / tail / lst))
      (if (= (list-length / lst) 2)
      (merge-list (head / lst) / (head / tail / lst))
      (if (= (list-length / lst) 1)
          (head / lst)
          (vector))));

equal (vector 1 2 3 4) (merge-list (vector 1 2) (vector 3 4));

equal (vector 1 2 3 4) (merge-lists (vector (vector 1 2) (vector 3) (vector 4)));

# helper for pairing

define prefix /
  ? x / 
  ? lst /
  map (? y (vector (x) (y))) (lst);

equal (vector (vector 1 10) (vector 1 11))
       (prefix 1 (vector 10 11));

# need a way to take product of domains

define pairing /
  ? lst1 / 
  ? lst2
  (if (> (list-length / lst1) 0)
      (merge-list (prefix (head / lst1) (lst2))
          (pairing (tail / lst1) (lst2)))
      (vector));

equal (vector (vector 1 10) (vector 1 11) (vector 2 10) (vector 2 11))
       (pairing (vector 1 2) (vector 10 11));

# need a way to make counting sets

define count /
  ? lo / ? hi
  (if (<= (lo) (hi))
      (prepend (lo) (count (+ (lo) 1) (hi)))
      (vector));

equal (vector 0 1 2 3 4) (count 0 4);

# given an image of a circuit, extract a model.
# wire elements are centered on multiples of 8

# individual element...

define distill-element /
  ? image / ? xlogic / ? ylogic / ? xmid / ? ymid 
  (if (image-get (image) (ymid) (xmid))
      (assign vert (image-get (image) (+ (ymid) 4) (xmid)) /
          assign dx (if (vert) 0 1) /
          assign dy (if (vert) 1 0) /
          assign pos (image-get (image) 
                    (+ (ymid) / + (* 4 / dy) (* 2 / dx))
                    (+ (xmid) / - (* 4 / dx) (* 2 / dy))) /
          assign sgn (if (pos) 1 (- 0 1)) /
          assign dx (* (sgn) (dx)) /
          assign dy (* (sgn) (dy)) /
          assign active (image-get (image) (+ (ymid) (dx)) (- (xmid) (dy))) /
          (vector 
           (vector (- (xlogic) (dx)) 
               (- (ylogic) (dy))
               (+ (xlogic) (dx))
               (+ (ylogic) (dy))
               (active))))
      (vector));

# full circuit...

define distill-circuit /
  ? image /
  assign h (div (image-height / image) 8) /
  assign w (div (image-width / image) 8) 
  (merge-lists
   (map (? v /
       assign xlogic (list-ref (v) 0) /
       assign ylogic (list-ref (v) 1) /
       assign xmid (* 8 / xlogic) /
       assign ymid (* 8 / ylogic) /
       distill-element (image) (xlogic) (ylogic) (xmid) (ymid))
    (pairing (count 1 (- (w) 1))
         (count 1 (- (h) 1)))));

43. testing alternate primer based on gates: cos_not circuit

# This section contains one or more representations of a circuit
# constructed using UNLESS gates.

define cos_not_gate / vector 
  (vector 0 6 2 6 (true))
  (vector 2 6 4 6 (true))
  (vector 4 6 6 6 (true))
  (vector 6 6 8 6 (true))
  (vector 8 4 8 6 (true))
  (vector 8 6 8 8 (false))
  (vector 8 8 10 8 (false))
  (vector 10 8 12 8 (false))
  (vector 12 8 12 6 (false))
  (vector 12 6 14 6 (false))
  (vector 14 6 16 6 (false))
  (vector 16 6 18 6 (false))
  (vector 18 6 20 6 (false));

define cos_not_image / make-image 109 169 / vector 
  (:::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:..............................................................:::......................................................................................................:)
  (:..............................................................:::......................................................................................................:)
  (:..............................................................:::......................................................................................................:)
  (:..............................................................:::......................................................................................................:)
  (:..............................................................:::......................................................................................................:)
  (:..............................................................:::......................................................................................................:)
  (:..............................................................:::......................................................................................................:)
  (:..............................................................:::......................................................................................................:)
  (:..............................................................:::......................................................................................................:)
  (:.............................................................:::::.....................................................................................................:)
  (:..............................................................:::......................................................................................................:)
  (:...........:...............:...............:...............:...:...........................................:...............:...............:...............:...........:)
  (:..:::::::::::.....:::::::::::.....:::::::::::.....:::::::::::..............................................::..............::..............::..............::..........:)
  (:..::::::::::::....::::::::::::....::::::::::::....::::::::::::....................................::::::::::::....::::::::::::....::::::::::::....::::::::::::.........:)
  (:..:::::::::::.....:::::::::::.....:::::::::::.....:::::::::::..............................................::..............::..............::..............::..........:)
  (:...........:...............:...............:...............:...................................:...........:...............:...............:...............:...........:)
  (:...............................................................:..............................:::......................................................................:)
  (:...............................................................:.............................:::::.....................................................................:)
  (:...............................................................:...............................:.......................................................................:)
  (:...............................................................:...............................:.......................................................................:)
  (:...............................................................:...............................:.......................................................................:)
  (:...............................................................:...............................:.......................................................................:)
  (:...............................................................:...............................:.......................................................................:)
  (:...............................................................:...............................:.......................................................................:)
  (:...............................................................:...............................:.......................................................................:)
  (:.............................................................:::::.............................:.......................................................................:)
  (:..............................................................:::..............................:.......................................................................:)
  (:...............................................................:...........:...............:...........................................................................:)
  (:...........................................................................::..............::..........................................................................:)
  (:..................................................................::::::::::::....::::::::::::.........................................................................:)
  (:...........................................................................::..............::..........................................................................:)
  (:...........................................................................:...............:...........................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::);

equal (cos_not_gate) (distill-circuit (cos_not_image));

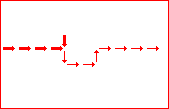
Run simulator

44. testing alternate primer based on gates: cos_and circuit

# This section contains one or more representations of a circuit
# constructed using UNLESS gates.

define cos_and_gate / vector 
  (vector 0 2 2 2 (true))
  (vector 0 8 2 8 (true))
  (vector 2 2 4 2 (true))
  (vector 2 4 4 4 (true))
  (vector 2 6 4 6 (true))
  (vector 2 8 4 8 (true))
  (vector 4 2 4 4 (true))
  (vector 4 8 4 6 (true))
  (vector 4 4 6 4 (false))
  (vector 4 6 6 6 (false))
  (vector 6 4 8 4 (false))
  (vector 6 6 8 6 (false))
  (vector 8 4 10 4 (false))
  (vector 8 6 10 6 (false))
  (vector 10 2 10 4 (true))
  (vector 10 4 10 6 (true))
  (vector 10 6 10 8 (true))
  (vector 10 8 12 8 (true))
  (vector 12 8 14 8 (true))
  (vector 14 8 16 8 (true))
  (vector 16 8 18 8 (true));

define cos_and_image / make-image 88 153 / vector 
  (:::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::)
  (:.......................................................................................................................................................:)
  (:.......................................................................................................................................................:)
  (:.......................................................................................................................................................:)
  (:.......................................................................................................................................................:)
  (:.......................................................................................................................................................:)
  (:.......................................................................................................................................................:)
  (:.......................................................................................................................................................:)
  (:.......................................................................................................................................................:)
  (:.......................................................................................................................................................:)
  (:.......................................................................................................................................................:)
  (:.......................................................................................................................................................:)
  (:.......................................................................................................................................................:)
  (:.......................................................................................................................................................:)
  (:...........:...............:...........................................................................................................................:)
  (:..:::::::::::.....:::::::::::..........................................................................................................................:)
  (:..::::::::::::....::::::::::::.........................................................................................................................:)
  (:..:::::::::::.....:::::::::::..........................................................................................................................:)
  (:...........:...............:...........................................................................................................................:)
  (:..............................:::.............................................:::......................................................................:)
  (:..............................:::.............................................:::......................................................................:)
  (:..............................:::.............................................:::......................................................................:)
  (:..............................:::.............................................:::......................................................................:)
  (:..............................:::.............................................:::......................................................................:)
  (:..............................:::.............................................:::......................................................................:)
  (:..............................:::.............................................:::......................................................................:)
  (:..............................:::.............................................:::......................................................................:)
  (:..............................:::.............................................:::......................................................................:)
  (:.............................:::::...........................................:::::.....................................................................:)
  (:..............................:::.............................................:::......................................................................:)
  (:...........................:...:...........:...............:...............:...:.......................................................................:)
  (:..................:::::::::::..............::..............::..............::..........................................................................:)
  (:..................::::::::::::....::::::::::::....::::::::::::....::::::::::::.........................................................................:)
  (:..................:::::::::::..............::..............::..............::..........................................................................:)
  (:...........................:...............:...............:...............:...........................................................................:)
  (:..............................................................................:::......................................................................:)
  (:..............................................................................:::......................................................................:)
  (:..............................................................................:::......................................................................:)
  (:..............................................................................:::......................................................................:)
  (:..............................................................................:::......................................................................:)
  (:..............................................................................:::......................................................................:)
  (:..............................................................................:::......................................................................:)
  (:..............................................................................:::......................................................................:)
  (:..............................................................................:::......................................................................:)
  (:.............................................................................:::::.....................................................................:)
  (:..............................................................................:::......................................................................:)
  (:...........................:...............:...............:...............:...:.......................................................................:)
  (:..................:::::::::::..............::..............::..............::..........................................................................:)
  (:..................::::::::::::....::::::::::::....::::::::::::....::::::::::::.........................................................................:)
  (:..................:::::::::::..............::..............::..............::..........................................................................:)
  (:...........................:...:...........:...............:...............:...........................................................................:)
  (:..............................:::.............................................:::......................................................................:)
  (:.............................:::::............................................:::......................................................................:)
  (:..............................:::.............................................:::......................................................................:)
  (:..............................:::.............................................:::......................................................................:)
  (:..............................:::.............................................:::......................................................................:)
  (:..............................:::.............................................:::......................................................................:)
  (:..............................:::.............................................:::......................................................................:)
  (:..............................:::.............................................:::......................................................................:)
  (:..............................:::.............................................:::......................................................................:)
  (:..............................:::............................................:::::.....................................................................:)
  (:..............................:::.............................................:::......................................................................:)
  (:...........:...............:...................................................:...........:...............:...............:...............:...........:)
  (:..:::::::::::.....:::::::::::.....................................................:::::::::::.....:::::::::::.....:::::::::::.....:::::::::::..........:)
  (:..::::::::::::....::::::::::::....................................................::::::::::::....::::::::::::....::::::::::::....::::::::::::.........:)
  (:..:::::::::::.....:::::::::::.....................................................:::::::::::.....:::::::::::.....:::::::::::.....:::::::::::..........:)
  (:...........:...............:...............................................................:...............:...............:...............:...........:)
  (:.......................................................................................................................................................:)
  (:.......................................................................................................................................................:)
  (:.......................................................................................................................................................:)
  (:.......................................................................................................................................................:)
  (:.......................................................................................................................................................:)
  (:.......................................................................................................................................................:)
  (:.......................................................................................................................................................:)
  (:.......................................................................................................................................................:)
  (:.......................................................................................................................................................:)
  (:.......................................................................................................................................................:)
  (:.......................................................................................................................................................:)
  (:.......................................................................................................................................................:)
  (:.......................................................................................................................................................:)
  (:.......................................................................................................................................................:)
  (:.......................................................................................................................................................:)
  (:.......................................................................................................................................................:)
  (:.......................................................................................................................................................:)
  (:.......................................................................................................................................................:)
  (:.......................................................................................................................................................:)
  (:.......................................................................................................................................................:)
  (:::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::);

equal (cos_and_gate) (distill-circuit (cos_and_image));

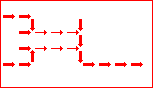
Run simulator

45. testing alternate primer based on gates: cos_or circuit

# This section contains one or more representations of a circuit
# constructed using UNLESS gates.

define cos_or_gate / vector 
  (vector 2 4 4 4 (true))
  (vector 2 6 4 6 (true))
  (vector 4 4 6 4 (true))
  (vector 4 6 6 6 (true))
  (vector 6 4 8 4 (true))
  (vector 6 6 8 6 (true))
  (vector 8 4 10 4 (true))
  (vector 8 6 10 6 (true))
  (vector 8 8 10 8 (true))
  (vector 10 2 10 4 (true))
  (vector 10 4 10 6 (false))
  (vector 10 6 10 8 (false))
  (vector 10 8 12 8 (true))
  (vector 12 8 14 8 (true))
  (vector 14 8 16 8 (true))
  (vector 16 8 18 8 (true));

define cos_or_image / make-image 93 169 / vector 
  (:::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:..............................................................................:::......................................................................................:)
  (:..............................................................................:::......................................................................................:)
  (:..............................................................................:::......................................................................................:)
  (:..............................................................................:::......................................................................................:)
  (:..............................................................................:::......................................................................................:)
  (:..............................................................................:::......................................................................................:)
  (:..............................................................................:::......................................................................................:)
  (:..............................................................................:::......................................................................................:)
  (:..............................................................................:::......................................................................................:)
  (:.............................................................................:::::.....................................................................................:)
  (:..............................................................................:::......................................................................................:)
  (:...........................:...............:...............:...............:...:.......................................................................................:)
  (:..................:::::::::::.....:::::::::::.....:::::::::::.....:::::::::::..........................................................................................:)
  (:..................::::::::::::....::::::::::::....::::::::::::....::::::::::::.........................................................................................:)
  (:..................:::::::::::.....:::::::::::.....:::::::::::.....:::::::::::..........................................................................................:)
  (:...........................:...............:...............:...............:...........................................................................................:)
  (:...............................................................................:.......................................................................................:)
  (:...............................................................................:.......................................................................................:)
  (:...............................................................................:.......................................................................................:)
  (:...............................................................................:.......................................................................................:)
  (:...............................................................................:.......................................................................................:)
  (:...............................................................................:.......................................................................................:)
  (:...............................................................................:.......................................................................................:)
  (:...............................................................................:.......................................................................................:)
  (:...............................................................................:.......................................................................................:)
  (:.............................................................................:::::.....................................................................................:)
  (:..............................................................................:::......................................................................................:)
  (:...........................:...............:...............:...............:...:.......................................................................................:)
  (:..................:::::::::::.....:::::::::::.....:::::::::::.....:::::::::::..........................................................................................:)
  (:..................::::::::::::....::::::::::::....::::::::::::....::::::::::::.........................................................................................:)
  (:..................:::::::::::.....:::::::::::.....:::::::::::.....:::::::::::..........................................................................................:)
  (:...........................:...............:...............:...............:...........................................................................................:)
  (:...............................................................................:.......................................................................................:)
  (:...............................................................................:.......................................................................................:)
  (:...............................................................................:.......................................................................................:)
  (:...............................................................................:.......................................................................................:)
  (:...............................................................................:.......................................................................................:)
  (:...............................................................................:.......................................................................................:)
  (:...............................................................................:.......................................................................................:)
  (:...............................................................................:.......................................................................................:)
  (:...............................................................................:.......................................................................................:)
  (:.............................................................................:::::.....................................................................................:)
  (:..............................................................................:::......................................................................................:)
  (:...........................................................................:...:...........:...............:...............:...............:...........................:)
  (:..................................................................:::::::::::.....:::::::::::.....:::::::::::.....:::::::::::.....:::::::::::..........................:)
  (:..................................................................::::::::::::....::::::::::::....::::::::::::....::::::::::::....::::::::::::.........................:)
  (:..................................................................:::::::::::.....:::::::::::.....:::::::::::.....:::::::::::.....:::::::::::..........................:)
  (:...........................................................................:...............:...............:...............:...............:...........................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::);

equal (cos_or_gate) (distill-circuit (cos_or_image));

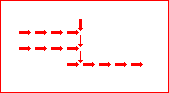
Run simulator

46. testing alternate primer based on gates: cos_nor circuit

# This section contains one or more representations of a circuit
# constructed using UNLESS gates.

define cos_nor_gate / vector 
  (vector 0 6 2 6 (true))
  (vector 0 8 2 8 (true))
  (vector 2 6 4 6 (true))
  (vector 2 8 4 8 (true))
  (vector 4 6 6 6 (true))
  (vector 4 8 6 8 (true))
  (vector 6 6 8 6 (true))
  (vector 6 8 8 8 (true))
  (vector 8 4 8 6 (true))
  (vector 8 6 8 8 (false))
  (vector 8 8 8 10 (false))
  (vector 8 10 10 10 (false))
  (vector 10 10 12 10 (false))
  (vector 12 10 14 10 (false))
  (vector 14 10 16 10 (false))
  (vector 16 10 18 10 (false))
  (vector 18 10 20 10 (false));

define cos_nor_image / make-image 125 169 / vector 
  (:::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:..............................................................:::......................................................................................................:)
  (:..............................................................:::......................................................................................................:)
  (:..............................................................:::......................................................................................................:)
  (:..............................................................:::......................................................................................................:)
  (:..............................................................:::......................................................................................................:)
  (:..............................................................:::......................................................................................................:)
  (:..............................................................:::......................................................................................................:)
  (:..............................................................:::......................................................................................................:)
  (:..............................................................:::......................................................................................................:)
  (:.............................................................:::::.....................................................................................................:)
  (:..............................................................:::......................................................................................................:)
  (:...........:...............:...............:...............:...:.......................................................................................................:)
  (:..:::::::::::.....:::::::::::.....:::::::::::.....:::::::::::..........................................................................................................:)
  (:..::::::::::::....::::::::::::....::::::::::::....::::::::::::.........................................................................................................:)
  (:..:::::::::::.....:::::::::::.....:::::::::::.....:::::::::::..........................................................................................................:)
  (:...........:...............:...............:...............:...........................................................................................................:)
  (:...............................................................:.......................................................................................................:)
  (:...............................................................:.......................................................................................................:)
  (:...............................................................:.......................................................................................................:)
  (:...............................................................:.......................................................................................................:)
  (:...............................................................:.......................................................................................................:)
  (:...............................................................:.......................................................................................................:)
  (:...............................................................:.......................................................................................................:)
  (:...............................................................:.......................................................................................................:)
  (:...............................................................:.......................................................................................................:)
  (:.............................................................:::::.....................................................................................................:)
  (:..............................................................:::......................................................................................................:)
  (:...........:...............:...............:...............:...:.......................................................................................................:)
  (:..:::::::::::.....:::::::::::.....:::::::::::.....:::::::::::..........................................................................................................:)
  (:..::::::::::::....::::::::::::....::::::::::::....::::::::::::.........................................................................................................:)
  (:..:::::::::::.....:::::::::::.....:::::::::::.....:::::::::::..........................................................................................................:)
  (:...........:...............:...............:...............:...........................................................................................................:)
  (:...............................................................:.......................................................................................................:)
  (:...............................................................:.......................................................................................................:)
  (:...............................................................:.......................................................................................................:)
  (:...............................................................:.......................................................................................................:)
  (:...............................................................:.......................................................................................................:)
  (:...............................................................:.......................................................................................................:)
  (:...............................................................:.......................................................................................................:)
  (:...............................................................:.......................................................................................................:)
  (:...............................................................:.......................................................................................................:)
  (:.............................................................:::::.....................................................................................................:)
  (:..............................................................:::......................................................................................................:)
  (:...............................................................:...........:...............:...............:...............:...............:...............:...........:)
  (:...........................................................................::..............::..............::..............::..............::..............::..........:)
  (:..................................................................::::::::::::....::::::::::::....::::::::::::....::::::::::::....::::::::::::....::::::::::::.........:)
  (:...........................................................................::..............::..............::..............::..............::..............::..........:)
  (:...........................................................................:...............:...............:...............:...............:...............:...........:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::);

equal (cos_nor_gate) (distill-circuit (cos_nor_image));

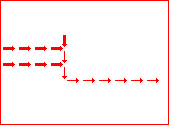
Run simulator

47. testing alternate primer based on gates: cos_osc circuit

# This section contains one or more representations of a circuit
# constructed using UNLESS gates.

define cos_osc_gate / vector 
  (vector 4 8 6 8 (true))
  (vector 6 8 8 8 (true))
  (vector 8 6 8 8 (true))
  (vector 10 6 8 6 (true))
  (vector 8 8 10 8 (false))
  (vector 12 6 10 6 (false))
  (vector 10 8 12 8 (false))
  (vector 12 8 12 6 (false))
  (vector 12 8 14 8 (false))
  (vector 14 8 16 8 (false));

define cos_osc_image / make-image 120 169 / vector 
  (:::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:...................................................................:...............:...................................................................................:)
  (:..................................................................:::::::::::.....::...................................................................................:)
  (:.................................................................::::::::::::....::::::::::::..........................................................................:)
  (:..................................................................:::::::::::.....::...................................................................................:)
  (:...................................................................:...............:...........:.......................................................................:)
  (:..............................................................:::.............................:::......................................................................:)
  (:..............................................................:::............................:::::.....................................................................:)
  (:..............................................................:::..............................:.......................................................................:)
  (:..............................................................:::..............................:.......................................................................:)
  (:..............................................................:::..............................:.......................................................................:)
  (:..............................................................:::..............................:.......................................................................:)
  (:..............................................................:::..............................:.......................................................................:)
  (:..............................................................:::..............................:.......................................................................:)
  (:..............................................................:::..............................:.......................................................................:)
  (:.............................................................:::::.............................:.......................................................................:)
  (:..............................................................:::..............................:.......................................................................:)
  (:...........................................:...............:...:...........:...............:...............:...............:...........................................:)
  (:..................................:::::::::::.....:::::::::::..............::..............::..............::..............::..........................................:)
  (:..................................::::::::::::....::::::::::::....::::::::::::....::::::::::::....::::::::::::....::::::::::::.........................................:)
  (:..................................:::::::::::.....:::::::::::..............::..............::..............::..............::..........................................:)
  (:...........................................:...............:...............:...............:...............:...............:...........................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::);

equal (cos_osc_gate) (distill-circuit (cos_osc_image));

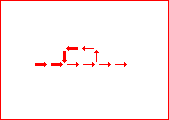
Run simulator

48. testing alternate primer based on gates: cos_sr circuit

# This section contains one or more representations of a circuit
# constructed using UNLESS gates.

define cos_sr_gate / vector 
  (vector 0 2 2 2 (true))
  (vector 0 8 2 8 (true))
  (vector 2 2 4 2 (true))
  (vector 2 8 4 8 (true))
  (vector 4 2 6 2 (true))
  (vector 4 6 6 6 (true))
  (vector 4 8 6 8 (true))
  (vector 6 8 6 6 (true))
  (vector 6 2 8 2 (true))
  (vector 6 6 8 6 (false))
  (vector 8 4 8 6 (false))
  (vector 8 2 10 2 (true))
  (vector 10 4 8 4 (false))
  (vector 8 6 10 6 (false))
  (vector 10 6 10 8 (false))
  (vector 10 2 12 2 (true))
  (vector 12 4 10 4 (false))
  (vector 10 6 12 6 (false))
  (vector 10 8 12 8 (false))
  (vector 12 6 12 4 (false))
  (vector 12 2 14 2 (true))
  (vector 14 4 12 4 (false))
  (vector 12 8 14 8 (false))
  (vector 14 2 14 4 (true))
  (vector 16 4 14 4 (true))
  (vector 14 8 16 8 (false))
  (vector 16 8 18 8 (false))
  (vector 18 8 20 8 (false));

define cos_sr_image / make-image 88 169 / vector 
  (:::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:...........:...............:...............:...............:...............:...............:...............:...........................................................:)
  (:..:::::::::::.....:::::::::::.....:::::::::::.....:::::::::::.....:::::::::::.....:::::::::::.....:::::::::::..........................................................:)
  (:..::::::::::::....::::::::::::....::::::::::::....::::::::::::....::::::::::::....::::::::::::....::::::::::::.........................................................:)
  (:..:::::::::::.....:::::::::::.....:::::::::::.....:::::::::::.....:::::::::::.....:::::::::::.....:::::::::::..........................................................:)
  (:...........:...............:...............:...............:...............:...............:...............:...........................................................:)
  (:..............................................................................................................:::......................................................:)
  (:..............................................................................................................:::......................................................:)
  (:..............................................................................................................:::......................................................:)
  (:..............................................................................................................:::......................................................:)
  (:..............................................................................................................:::......................................................:)
  (:..............................................................................................................:::......................................................:)
  (:..............................................................................................................:::......................................................:)
  (:..............................................................................................................:::......................................................:)
  (:..............................................................................................................:::......................................................:)
  (:.............................................................................................................:::::.....................................................:)
  (:..............................................................................................................:::......................................................:)
  (:...................................................................:...............:...............:...........:...:...................................................:)
  (:..................................................................::..............::..............::..............:::::::::::..........................................:)
  (:.................................................................::::::::::::....::::::::::::....::::::::::::....::::::::::::..........................................:)
  (:..................................................................::..............::..............::..............:::::::::::..........................................:)
  (:...................................................................:...............:...........:...:...............:...................................................:)
  (:...............................................................:..............................:::......................................................................:)
  (:...............................................................:.............................:::::.....................................................................:)
  (:...............................................................:...............................:.......................................................................:)
  (:...............................................................:...............................:.......................................................................:)
  (:...............................................................:...............................:.......................................................................:)
  (:...............................................................:...............................:.......................................................................:)
  (:...............................................................:...............................:.......................................................................:)
  (:...............................................................:...............................:.......................................................................:)
  (:...............................................................:...............................:.......................................................................:)
  (:.............................................................:::::.............................:.......................................................................:)
  (:..............................................................:::..............................:.......................................................................:)
  (:...........................................:...............:...:...........:...............:...........................................................................:)
  (:..................................:::::::::::..............::..............::..............::..........................................................................:)
  (:..................................::::::::::::....::::::::::::....::::::::::::....::::::::::::.........................................................................:)
  (:..................................:::::::::::..............::..............::..............::..........................................................................:)
  (:...........................................:...:...........:...............:...............:...........................................................................:)
  (:..............................................:::..............................:.......................................................................................:)
  (:.............................................:::::.............................:.......................................................................................:)
  (:..............................................:::..............................:.......................................................................................:)
  (:..............................................:::..............................:.......................................................................................:)
  (:..............................................:::..............................:.......................................................................................:)
  (:..............................................:::..............................:.......................................................................................:)
  (:..............................................:::..............................:.......................................................................................:)
  (:..............................................:::..............................:.......................................................................................:)
  (:..............................................:::..............................:.......................................................................................:)
  (:..............................................:::............................:::::.....................................................................................:)
  (:..............................................:::.............................:::......................................................................................:)
  (:...........:...............:...............:...................................:...........:...............:...............:...............:...............:...........:)
  (:..:::::::::::.....:::::::::::.....:::::::::::..............................................::..............::..............::..............::..............::..........:)
  (:..::::::::::::....::::::::::::....::::::::::::....................................::::::::::::....::::::::::::....::::::::::::....::::::::::::....::::::::::::.........:)
  (:..:::::::::::.....:::::::::::.....:::::::::::..............................................::..............::..............::..............::..............::..........:)
  (:...........:...............:...............:...............................................:...............:...............:...............:...............:...........:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::);

equal (cos_sr_gate) (distill-circuit (cos_sr_image));

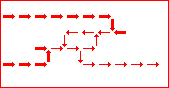
Run simulator

49. testing alternate primer based on gates: cos_d circuit

# This section contains one or more representations of a circuit
# constructed using UNLESS gates.

define cos_d_gate / vector 
  (vector 0 2 2 2 (true))
  (vector 0 6 2 6 (true))
  (vector 2 2 4 2 (true))
  (vector 2 6 4 6 (true))
  (vector 4 2 6 2 (true))
  (vector 4 6 6 6 (true))
  (vector 6 2 8 2 (true))
  (vector 6 6 8 6 (true))
  (vector 8 2 10 2 (true))
  (vector 8 6 10 6 (true))
  (vector 10 6 10 4 (true))
  (vector 10 10 10 8 (true))
  (vector 10 2 12 2 (true))
  (vector 10 4 12 4 (true))
  (vector 10 6 12 6 (true))
  (vector 10 8 12 8 (true))
  (vector 12 10 10 10 (true))
  (vector 12 0 12 2 (true))
  (vector 12 2 12 4 (false))
  (vector 12 6 12 8 (true))
  (vector 12 10 12 12 (true))
  (vector 12 4 14 4 (true))
  (vector 12 8 14 8 (false))
  (vector 14 10 12 10 (true))
  (vector 12 12 14 12 (true))
  (vector 14 0 14 2 (true))
  (vector 14 2 14 4 (true))
  (vector 14 4 14 6 (false))
  (vector 14 6 14 8 (false))
  (vector 14 8 14 10 (false))
  (vector 16 10 14 10 (true))
  (vector 14 12 16 12 (true))
  (vector 16 12 18 12 (true))
  (vector 18 12 20 12 (true));

define cos_d_image / make-image 109 169 / vector 
  (:::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:..............................................................................................:::.............:::......................................................:)
  (:..............................................................................................:::.............:::......................................................:)
  (:..............................................................................................:::.............:::......................................................:)
  (:..............................................................................................:::.............:::......................................................:)
  (:..............................................................................................:::.............:::......................................................:)
  (:..............................................................................................:::.............:::......................................................:)
  (:..............................................................................................:::.............:::......................................................:)
  (:..............................................................................................:::.............:::......................................................:)
  (:..............................................................................................:::.............:::......................................................:)
  (:.............................................................................................:::::...........:::::.....................................................:)
  (:..............................................................................................:::.............:::......................................................:)
  (:...........:...............:...............:...............:...............:...............:...:...............:.......................................................:)
  (:..:::::::::::.....:::::::::::.....:::::::::::.....:::::::::::.....:::::::::::.....:::::::::::..........................................................................:)
  (:..::::::::::::....::::::::::::....::::::::::::....::::::::::::....::::::::::::....::::::::::::.........................................................................:)
  (:..:::::::::::.....:::::::::::.....:::::::::::.....:::::::::::.....:::::::::::.....:::::::::::..........................................................................:)
  (:...........:...............:...............:...............:...............:...............:...........................................................................:)
  (:...............................................................................................:..............:::......................................................:)
  (:...............................................................................................:..............:::......................................................:)
  (:...............................................................................................:..............:::......................................................:)
  (:...............................................................................................:..............:::......................................................:)
  (:...............................................................................................:..............:::......................................................:)
  (:...............................................................................................:..............:::......................................................:)
  (:...............................................................................................:..............:::......................................................:)
  (:...............................................................................................:..............:::......................................................:)
  (:...............................................................................................:..............:::......................................................:)
  (:.............................................................................................:::::...........:::::.....................................................:)
  (:..............................................................................................:::.............:::......................................................:)
  (:...........................................................................................:...:...........:...:.......................................................:)
  (:..................................................................................:::::::::::.....:::::::::::..........................................................:)
  (:..................................................................................::::::::::::....::::::::::::.........................................................:)
  (:..................................................................................:::::::::::.....:::::::::::..........................................................:)
  (:...............................................................................:...........:...............:...........................................................:)
  (:..............................................................................:::..............................:.......................................................:)
  (:.............................................................................:::::.............................:.......................................................:)
  (:..............................................................................:::..............................:.......................................................:)
  (:..............................................................................:::..............................:.......................................................:)
  (:..............................................................................:::..............................:.......................................................:)
  (:..............................................................................:::..............................:.......................................................:)
  (:..............................................................................:::..............................:.......................................................:)
  (:..............................................................................:::..............................:.......................................................:)
  (:..............................................................................:::..............................:.......................................................:)
  (:..............................................................................:::............................:::::.....................................................:)
  (:..............................................................................:::.............................:::......................................................:)
  (:...........:...............:...............:...............:...............:...............:...................:.......................................................:)
  (:..:::::::::::.....:::::::::::.....:::::::::::.....:::::::::::.....:::::::::::.....:::::::::::..........................................................................:)
  (:..::::::::::::....::::::::::::....::::::::::::....::::::::::::....::::::::::::....::::::::::::.........................................................................:)
  (:..:::::::::::.....:::::::::::.....:::::::::::.....:::::::::::.....:::::::::::.....:::::::::::..........................................................................:)
  (:...........:...............:...............:...............:...............:...............:...........................................................................:)
  (:..............................................................................................:::..............:.......................................................:)
  (:..............................................................................................:::..............:.......................................................:)
  (:..............................................................................................:::..............:.......................................................:)
  (:..............................................................................................:::..............:.......................................................:)
  (:..............................................................................................:::..............:.......................................................:)
  (:..............................................................................................:::..............:.......................................................:)
  (:..............................................................................................:::..............:.......................................................:)
  (:..............................................................................................:::..............:.......................................................:)
  (:..............................................................................................:::..............:.......................................................:)
  (:.............................................................................................:::::...........:::::.....................................................:)
  (:..............................................................................................:::.............:::......................................................:)
  (:...........................................................................................:...:...........:...:.......................................................:)
  (:..................................................................................:::::::::::..............::..........................................................:)
  (:..................................................................................::::::::::::....::::::::::::.........................................................:)
  (:..................................................................................:::::::::::..............::..........................................................:)
  (:...............................................................................:...........:...............:...........................................................:)
  (:..............................................................................:::..............................:.......................................................:)
  (:.............................................................................:::::.............................:.......................................................:)
  (:..............................................................................:::..............................:.......................................................:)
  (:..............................................................................:::..............................:.......................................................:)
  (:..............................................................................:::..............................:.......................................................:)
  (:..............................................................................:::..............................:.......................................................:)
  (:..............................................................................:::..............................:.......................................................:)
  (:..............................................................................:::..............................:.......................................................:)
  (:..............................................................................:::..............................:.......................................................:)
  (:..............................................................................:::............................:::::.....................................................:)
  (:..............................................................................:::.............................:::......................................................:)
  (:...................................................................................:...............:...........:...:...................................................:)
  (:..................................................................................:::::::::::.....:::::::::::.....:::::::::::..........................................:)
  (:.................................................................................::::::::::::....::::::::::::....::::::::::::..........................................:)
  (:..................................................................................:::::::::::.....:::::::::::.....:::::::::::..........................................:)
  (:...................................................................................:...............:...............:...................................................:)
  (:..............................................................................................:::......................................................................:)
  (:..............................................................................................:::......................................................................:)
  (:..............................................................................................:::......................................................................:)
  (:..............................................................................................:::......................................................................:)
  (:..............................................................................................:::......................................................................:)
  (:..............................................................................................:::......................................................................:)
  (:..............................................................................................:::......................................................................:)
  (:..............................................................................................:::......................................................................:)
  (:..............................................................................................:::......................................................................:)
  (:.............................................................................................:::::.....................................................................:)
  (:..............................................................................................:::......................................................................:)
  (:...............................................................................................:...........:...............:...............:...............:...........:)
  (:..................................................................................................:::::::::::.....:::::::::::.....:::::::::::.....:::::::::::..........:)
  (:..................................................................................................::::::::::::....::::::::::::....::::::::::::....::::::::::::.........:)
  (:..................................................................................................:::::::::::.....:::::::::::.....:::::::::::.....:::::::::::..........:)
  (:...........................................................................................................:...............:...............:...............:...........:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:.......................................................................................................................................................................:)
  (:::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::);

equal (cos_d_gate) (distill-circuit (cos_d_image));

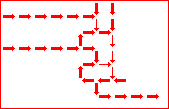
Run simulator

50. probing networks of unless gates

define set-input /
  ? circuit /
  ? index /
  ? value /
  assign wire (list-ref (circuit) (index)) 
  (map (? w (if (equal (w) (wire))
        (vector (list-ref (w) 0)
            (list-ref (w) 1)
            (list-ref (w) 2)            
            (list-ref (w) 3)
            (value))
        (w)))
       (circuit));

define read-output /
  ? circuit /
  ? index /
  assign len (list-length / circuit) /
  assign wire (list-ref (circuit) / - (- (len) 1) (index)) /
  list-ref (wire) 4;

define sim /
  ? circuit / ? steps / ? setter
  (if (> (steps) 0)
      (sim (simulate-unless (setter / circuit)) (- (steps) 1) (setter))
      (circuit));

define smart-sim /
  ? circuit /
  ? setter /
  sim (circuit) (list-length / circuit) (setter);

# test cos_not gate

define cos_not_harness /
  ? x /
  assign c (cos_not_gate) / 
  assign c (smart-sim (c) (? c (set-input (c) 0 (x)))) /
  read-output (c) 0;

= (false) / cos_not_harness / true;

= (true) / cos_not_harness / false;

# test cos_and gate

define cos_and_harness /
  ? x / ? y /
  assign c (cos_and_gate) / 
  assign c (smart-sim (c) (? c (set-input (set-input (c) 0 (x)) 1 (y)))) /
  read-output (c) 0;

= (false) / cos_and_harness (false) (false);

= (false) / cos_and_harness (false) (true);

= (false) / cos_and_harness (true) (false);

= (true) / cos_and_harness (true) (true);

# this code is more awkward than it needs to be -
# should make circuits mutable

51. end of part 3, start of part 4

# The following parts of the message start
# to introduce some self-reference into the message

intro part4;

52. a mechanism for referring to parts of the message

# Many choices for how to do this.
# Could do it without special machinery by using the
# standard A-B trick for giving e.g. a Turing machine
# access to its own description.
# Instead, will simply introduce a "primer" function
# that gives access to every statement made so far 
# (question: should future statements be included? 
# tentatively assume YES: will simplify
# discussion of creating modified copies of the
# complete message).

# For now, assume primer is a list of statements,
# with each statement being a list in the same
# form as "translate" functions expect.
# This means that there is, for now, no
# distinction between unary or binary,
# and the "/" structure is expanded.

intro primer;

# this line is referred to later - change/move carefully

equal (list-ref (primer) 0) (vector intro 1);

equal (list-ref (primer) 1) (vector intro 2);

equal (list-ref (primer) 2) (vector intro 3);

assign idx (list-find (primer) (vector intro primer) (? x 0)) 
    (equal (list-ref (primer) (+ (idx) 1))
           (vector equal 
               (vector list-ref (vector primer) 0)
               (vector vector intro 1)));

# Now, we could return to the MUD, simulate an agent A
# transferring a copy of the primer to another agent B,
# and then show B making a modified copy of that primer
# and passing it back to A.

# We could also show agents experimenting with the
# primer in various ways.

# Message is pretty solid up to this point.
# For testing purposes, useful to save state here to disk,
# command: DISK-SAVE base

53. some preparatory work for integrating with Java code

class Object ()
       (method add-one (lambda (x) (+ (x) 1)))
       (method unknown (lambda (x) (x)))
       (method <init>-V (self))
       (method <init> (self))
       (method classname Object)
       (method equals-Object-Z (this ==))
       (method equals (self equals-Object-Z))
       (method act (true))
       (method isobj (true));

define java-object / Object;

define act / ? x / true;

#(class java-string ()
#       (field super (java-object new))
#       (method classname String)
#       (method unknown (lambda (x) (super (x)))));

# inconsistency of various kinds of equality throughout message
# needs to be cleaned up

class Integer ()
       (field super (java-object new))
       (field value (cell new 0))
       (method <init> (self))
       (method <init>-V (self))
       (method <init>-I-V (lambda (v) 
                (begin 
                  (value set (v))
                  (self))))
       (method intValue-V (value get))
       (method intValue (self intValue-V))
       (method equals-Object-Z (lambda (o) (if (= (o classname) Integer)
                           (= (value get) (o value get))
                           (false))))
       (method equals (self equals-Object-Z))
       (method get (value get))
       (method set (lambda(x)
             (value set
                (if (number? / x)
                (x)
                (x intValue)))))
       (method classname Integer)
       (method unknown (lambda (x) (super (x))));

# string is basically the same as an integer

class String ()
       (field super (java-object new))
       (field value (cell new 0))
       (method <init> (self))
       (method <init>-V (self))
       (method <init>-String-V (lambda (v) 
                 (begin 
                   (value set (v value get))
                   (self))))
       (method int-init (lambda (x) 
              (begin 
                (value set (x))
                (self))))
       (method intValue-V (value get))
       (method intValue (self intValue-V))
       (method get (value get))
       (method set (lambda(x)
             (value set
                (if (number? / x)
                (x)
                (x intValue)))))
       (method equals-Object-Z (lambda (o) (if (= (o classname) String)
                           (= (value get) (o value get))
                           (false))))
       (method equals (self equals-Object-Z))
       (method classname String)
       (method unknown (lambda (x) (super (x))));

# will need to install class hierarchy, just hardcode a few things for now

define java
  (? x / ? y 
     (cond ((= (y) String) (String))
       ((= (y) Object) (java-object))
       ((= (y) Integer) (Integer))
       (java-object)));

(java util String) new isobj;

= ((java util String) new add-one 15) 16;

class java-numeric ()
       (field super (java-object new))
       (method unknown (lambda (x) (super (x))))
       (field java-content (cell new 0))
       (method get (java-content get))
       (method init (lambda (v)
              (begin
            (self set (v))
            (self))))
       (method set (lambda (v) (java-content set (v))));

define byte (java-numeric);

define char (java-numeric);

define double (java-numeric);

define float (java-numeric);

define int (java-numeric);

define long (java-numeric);

define short (java-numeric);

define boolean (java-numeric);

define void (java-numeric);

define java-test1 (int new);

java-test1 set 15;

= 15 (java-test1 get);

define java-test2 (int new init 17);

= 17 (java-test2 get);

define state-machine-test1
  (? x
     (cond ((= (x) 1) 20)
       ((= (x) 2) 40)
       ((= (x) 3) 60)
       0));

= (state-machine-test1 3) 60;

# really ought to go back and be clear about eager/laziness issues

define state-machine-test2
  (? x
     (cond ((= (x) 1) (java-test1 set 20))
       ((= (x) 2) (java-test1 set 40))
       ((= (x) 3) (java-test1 set 60))
       0));

state-machine-test2 2;

= (java-test1 get) 40;

define compare-object-reference
  (lambda (o1 o2)
    (if (number? / o1)
    (number? / o2)
    (= (o1 unique-id) (o2 unique-id))));

define jvm-maker
  (lambda (vars stack pc ret)
    (? op
     (begin
       (pc set (+ (pc get) 1)) /
     cond ((= (op) new)
        (lambda (type)
          (stack-push (stack) ((type) new))))
       ((= (op) dup)
        (stack-push (stack) (stack-peek (stack))))
       ((= (op) checkcast)
        (lambda (t)
          1))
       ((or (= (op) astore) (= (op) istore))
        (lambda (index)
          (vars set (hash-add (vars get) (index) (stack-pop (stack))))))
       ((or (= (op) aload) (= (op) iload))
        (lambda (index)
          (stack-push (stack) (hash-ref (vars get) (index)))))
       ((or (= (op) iconst) (= (op) ldc))
        (lambda (val)
          (stack-push (stack) (val))))
       ((= (op) aconst_null)
        (stack-push (stack) 0))
       ((= (op) instanceof)
        (lambda (t)
          (stack-push 
           (stack)
           (not / number? / (stack-pop / stack) (t new classname)))))
       ((= (op) getfield)
        (lambda (key ignore)
          (stack-push (stack) ((stack-pop (stack)) (key) get))))
       ((= (op) putfield)
        (lambda (key ignore)
          (let ((val (stack-pop (stack))))
        ((stack-pop (stack)) (key) set (val)))))
       ((= (op) imul)
        (let ((v2 (stack-pop (stack))))
          (let ((v1 (stack-pop (stack))))
        (stack-push (stack)
                (* (v1) (v2))))))
       ((= (op) iadd)
        (let ((v2 (stack-pop (stack))))
          (let ((v1 (stack-pop (stack))))
        (stack-push (stack)
                (+ (v1) (v2))))))
       ((= (op) isub)
        (let ((v2 (stack-pop (stack))))
          (let ((v1 (stack-pop (stack))))
        (stack-push (stack)
                (- (v1) (v2))))))
       ((= (op) goto)
        (lambda (x)
          (pc set (x))))
       ((= (op) iflt)
        (lambda (x)
          (if (< (stack-pop (stack)) 0)
          (pc set (x))
          0)))
       ((= (op) ifle)
        (lambda (x)
          (if (< (stack-pop (stack)) 1)
          (pc set (x))
          0)))
       ((= (op) ifgt)
        (lambda (x)
          (if (> (stack-pop (stack)) 0)
          (pc set (x))
          0)))
       ((= (op) ifge)
        (lambda (x)
          (if (>= (stack-pop (stack)) 0)
          (pc set (x))
          0)))
       ((= (op) ifne)
        (lambda (x)
          (if (not (= (stack-pop (stack)) 0))
          (pc set (x))
          0)))
       ((= (op) ifeq)
        (lambda (x)
          (if (= (stack-pop (stack)) 0)
          (pc set (x))
          0)))
       ((= (op) if_icmpne)
        (let ((v2 (stack-pop (stack))))
          (let ((v1 (stack-pop (stack))))
        (lambda (x)
          (if (not (= (v1) (v2)))
              (pc set (x))
              0)))))
       ((= (op) if_icmpeq)
        (let ((v2 (stack-pop (stack))))
          (let ((v1 (stack-pop (stack))))
        (lambda (x)
          (if (= (v1) (v2))
              (pc set (x))
              0)))))
       ((= (op) if_acmpne)
        (let ((v2 (stack-pop (stack))))
          (let ((v1 (stack-pop (stack))))
        (lambda (x)
          (if (not (compare-object-reference (v1) (v2)))
              (pc set (x))
              0)))))
       ((= (op) if_acmpeq)
        (let ((v2 (stack-pop (stack))))
          (let ((v1 (stack-pop (stack))))
        (lambda (x)
          (if (compare-object-reference (v1) (v2))
              (pc set (x))
              0)))))
       ((= (op) if_icmpge)
        (let ((v2 (stack-pop (stack))))
          (let ((v1 (stack-pop (stack))))
        (lambda (x)
          (if (>= (v1) (v2))
              (pc set (x))
              0)))))
       ((= (op) if_icmpgt)
        (let ((v2 (stack-pop (stack))))
          (let ((v1 (stack-pop (stack))))
        (lambda (x)
          (if (> (v1) (v2))
              (pc set (x))
              0)))))
       ((= (op) if_icmple)
        (let ((v2 (stack-pop (stack))))
          (let ((v1 (stack-pop (stack))))
        (lambda (x)
          (if (<= (v1) (v2))
              (pc set (x))
              0)))))
       ((= (op) if_icmplt)
        (let ((v2 (stack-pop (stack))))
          (let ((v1 (stack-pop (stack))))
        (lambda (x)
          (if (< (v1) (v2))
              (pc set (x))
              0)))))
       ((= (op) ifnull)
        (lambda (x)
          (if (number? / stack-pop (stack))
          (pc set (x))
          0)))
       ((= (op) ifnonnull)
        (lambda (x)
          (if (not (number? / stack-pop (stack)))
          (pc set (x))
          0)))
       ((= (op) return)
        (begin (ret set (hash-ref (vars get) 0))
           (pc set -1)))
       ((= (op) ireturn)
        (begin (ret set (stack-pop (stack)))
           (pc set -1)))
       ((= (op) areturn)
        (begin (ret set (stack-pop (stack)))
           (pc set -1)))
       ((= (op) goto)
        (lambda (target)
          (pc set (target))))
       ((= (op) invokevirtual)
        (lambda (target m n)
          (let ((result (stack-call (stack) (target) (m))))
        (if (= (n) 1)
            (stack-push (stack) (result))
            0))))
       ((= (op) invokeinterface)
        (lambda (target m n ignore)
          (let ((result (stack-call (stack) (target) (m))))
        (if (= (n) 1)
            (stack-push (stack) (result))
            0))))
       ((= (op) invokespecial)
        (lambda (target m n)
          (let ((result (stack-call-special (stack) 
                        (hash-ref (vars get) 0)
                        (target) 
                        (m))))
        (if (= (n) 1)
            (stack-push (stack) (result))
            0))))
       0)));

define stack-call
  (lambda (stack target ct)
    (if (= (ct) 0)
    ((stack-pop (stack)) (target))
    (let ((arg (stack-pop (stack))))
      ((stack-call (stack) (target) (- (ct) 1)) (arg)))));

define stack-call-special
  (lambda (stack self target ct)
    (if (= (ct) 0)
    (let ((act (stack-pop / stack)))
      (if (act == (self))
          (act super (target))
          (act (target))))
    (let ((arg (stack-pop (stack))))
      ((stack-call-special (stack) (self) (target) (- (ct) 1)) (arg)))));

define stack-push
  (lambda (stack x)
    (stack set (prepend (x) (stack get))));

define stack-pop
  (lambda (stack)
    (let ((v (head (stack get))))
      (begin
    (stack set (tail (stack get)))
    (v))));

define stack-peek
  (lambda (stack)
    (head (stack get)));

define stack-test1 (cell new (vector 5 3 1));

= (stack-pop (stack-test1)) 5;

= (stack-peek (stack-test1)) 3;

= (stack-pop (stack-test1)) 3;

stack-push (stack-test1) 7;

= (stack-pop (stack-test1)) 7;

define vars-test1 (cell new (hash-null));

define pc-test1 (cell new 0);

define ret-test1 (cell new 0);

define test-jvm (jvm-maker (vars-test1) (stack-test1) (pc-test1) (ret-test1));

stack-push (stack-test1) 4;

test-jvm dup;

= (stack-pop (stack-test1)) 4;

= (stack-pop (stack-test1)) 4;

stack-push (stack-test1) 66;

stack-push (stack-test1) 77;

test-jvm astore 3;

= (stack-pop (stack-test1)) 66;

test-jvm aload 3;

= (stack-pop (stack-test1)) 77;

class test-class ()
       (field x ((int) new))
       (field y ((int) new));

define test-this (test-class new);

test-this x set 5;

= (test-this x get) 5;

stack-push (stack-test1) (test-this);

= ((stack-pop (stack-test1)) x get) 5;

stack-push (stack-test1) (test-this);

test-jvm astore 0;

test-jvm aload 0;

test-jvm getfield x (int);

= (stack-pop (stack-test1)) 5;

test-jvm aload 0;

test-jvm iconst 15;

test-jvm putfield y (int);

= (test-this y get) 15;

stack-push (stack-test1) 7;

stack-push (stack-test1) 10;

test-jvm imul;

test-jvm ireturn;

= (ret-test1 get) 70;

define state-machine-helper /
  ? at /
  lambda (vars stack machine) /
  let ((pc (cell new (at)))
       (ret (cell new (true)))) /
  let ((jvm (jvm-maker (vars) (stack) (pc) (ret))))
  (begin
    (machine (jvm) (pc get))
    (if (= (pc get) -1)
    (ret get)
    (state-machine-helper (pc get) (vars) (stack) (machine))));

define state-machine
  (state-machine-helper 0);

stack-push (stack-test1) 10;

stack-push (stack-test1) 33;

= (state-machine (vars-test1) (stack-test1) / ? jvm / ? x
          (cond ((= (x) 0) (jvm istore 4))
            ((= (x) 1) (jvm iload 4))
            (jvm ireturn)))
   33;

stack-push (stack-test1) 10;

define bytecode-test-mul
  (lambda (arg0 arg1) /
      let ((vars / cell new / make-hash / vector (pair 0 0) (pair 1 (arg0)) (pair 2 (arg1)))
           (stack / cell new / vector)) /
           state-machine (vars) (stack) / ? jvm / ? x / cond
           ((= (x) 0) (jvm iload 1))
           ((= (x) 1) (jvm iload 2))
           ((= (x) 2) (jvm imul))
           ((= (x) 3) (jvm ireturn))
           (jvm return));

= (bytecode-test-mul 5 9) 45;

54. class translation 'COS_JavaTest'

# Sun Mar 23 02:45:09 CET 2014
# Produced by Fritzifier, based on JasminVisitor
# Using BCEL library to read Java bytecode
# Here is the original code:
# public class COS_JavaTest {
#     private int q = 0;
#     public int add(int x, int y) {
#     return x+y;
#     }
#     public int sub(int x, int y) {
#     return x-y;
#     }
#     public int mult(int x, int y) {
#     return x*y;
#     }
#     public int addmult(int x, int y, int z) {
#     return add(x,mult(y,z));
#     }
#     public void set(int x) {
#     q = x;
#     }
#     public int get() {
#     return q;
#     }
#     public int fact(int x) {
#     return (x>0)?(x*fact(sub(x,1))):1;
#     }
# }
# 

class COS_JavaTest ()
   (field super-ref (make-cell 0))
   (method new (set! (super-ref) ((java lang Object) / this)))
   (method super (? x / (get! / super-ref) / x))
   (method unknown (? x / self super / x))
   (field q ((int) new))
   (method <init>-V
     (lambda () /
      let ((vars / cell new / make-hash / vector
                    (pair 0 (self)))
           (stack / cell new / vector)) /
      state-machine (vars) (stack) / ? jvm / ? x / cond
         ((= (x) 0) (jvm aload 0))
         ((= (x) 1) (jvm invokespecial <init>-V 0 0))
         ((= (x) 2) (jvm aload 0))
         ((= (x) 3) (jvm iconst 0))
         ((= (x) 4) (jvm putfield q (int)))
         ((= (x) 5) (jvm return))
         (jvm return))
   )

   (method <init> (self <init>-V))

   (method add-I-I-I
     (lambda (arg0 arg1) /
      let ((vars / cell new / make-hash / vector
                    (pair 0 (self)) (pair 1 (arg0)) (pair 2 (arg1)))
           (stack / cell new / vector)) /
      state-machine (vars) (stack) / ? jvm / ? x / cond
         ((= (x) 0) (jvm iload 1))
         ((= (x) 1) (jvm iload 2))
         ((= (x) 2) (jvm iadd))
         ((= (x) 3) (jvm ireturn))
         (jvm return))
   )

   (method add (self add-I-I-I))

   (method sub-I-I-I
     (lambda (arg0 arg1) /
      let ((vars / cell new / make-hash / vector
                    (pair 0 (self)) (pair 1 (arg0)) (pair 2 (arg1)))
           (stack / cell new / vector)) /
      state-machine (vars) (stack) / ? jvm / ? x / cond
         ((= (x) 0) (jvm iload 1))
         ((= (x) 1) (jvm iload 2))
         ((= (x) 2) (jvm isub))
         ((= (x) 3) (jvm ireturn))
         (jvm return))
   )

   (method sub (self sub-I-I-I))

   (method mult-I-I-I
     (lambda (arg0 arg1) /
      let ((vars / cell new / make-hash / vector
                    (pair 0 (self)) (pair 1 (arg0)) (pair 2 (arg1)))
           (stack / cell new / vector)) /
      state-machine (vars) (stack) / ? jvm / ? x / cond
         ((= (x) 0) (jvm iload 1))
         ((= (x) 1) (jvm iload 2))
         ((= (x) 2) (jvm imul))
         ((= (x) 3) (jvm ireturn))
         (jvm return))
   )

   (method mult (self mult-I-I-I))

   (method addmult-I-I-I-I
     (lambda (arg0 arg1 arg2) /
      let ((vars / cell new / make-hash / vector
                    (pair 0 (self)) (pair 1 (arg0)) (pair 2 (arg1)) (pair 3 (arg2)))
           (stack / cell new / vector)) /
      state-machine (vars) (stack) / ? jvm / ? x / cond
         ((= (x) 0) (jvm aload 0))
         ((= (x) 1) (jvm iload 1))
         ((= (x) 2) (jvm aload 0))
         ((= (x) 3) (jvm iload 2))
         ((= (x) 4) (jvm iload 3))
         ((= (x) 5) (jvm invokevirtual mult-I-I-I 2 1))
         ((= (x) 6) (jvm invokevirtual add-I-I-I 2 1))
         ((= (x) 7) (jvm ireturn))
         (jvm return))
   )

   (method addmult (self addmult-I-I-I-I))

   (method set-I-V
     (lambda (arg0) /
      let ((vars / cell new / make-hash / vector
                    (pair 0 (self)) (pair 1 (arg0)))
           (stack / cell new / vector)) /
      state-machine (vars) (stack) / ? jvm / ? x / cond
         ((= (x) 0) (jvm aload 0))
         ((= (x) 1) (jvm iload 1))
         ((= (x) 2) (jvm putfield q (int)))
         ((= (x) 3) (jvm return))
         (jvm return))
   )

   (method set (self set-I-V))

   (method get-I
     (lambda () /
      let ((vars / cell new / make-hash / vector
                    (pair 0 (self)))
           (stack / cell new / vector)) /
      state-machine (vars) (stack) / ? jvm / ? x / cond
         ((= (x) 0) (jvm aload 0))
         ((= (x) 1) (jvm getfield q (int)))
         ((= (x) 2) (jvm ireturn))
         (jvm return))
   )

   (method get (self get-I))

   (method fact-I-I
     (lambda (arg0) /
      let ((vars / cell new / make-hash / vector
                    (pair 0 (self)) (pair 1 (arg0)))
           (stack / cell new / vector)) /
      state-machine (vars) (stack) / ? jvm / ? x / cond
         ((= (x) 0) (jvm iload 1))
         ((= (x) 1) (jvm ifle 11))
         ((= (x) 2) (jvm iload 1))
         ((= (x) 3) (jvm aload 0))
         ((= (x) 4) (jvm aload 0))
         ((= (x) 5) (jvm iload 1))
         ((= (x) 6) (jvm iconst 1))
         ((= (x) 7) (jvm invokevirtual sub-I-I-I 2 1))
         ((= (x) 8) (jvm invokevirtual fact-I-I 1 1))
         ((= (x) 9) (jvm imul))
         ((= (x) 10) (jvm goto 12))
         ((= (x) 11) (jvm iconst 1))
         ((= (x) 12) (jvm ireturn))
         (jvm return))
   )

   (method fact (self fact-I-I))

 ;

55. check that automatic conversion is workable

define test1 (COS_JavaTest new);

# Note that the names of methods include type information.
# This could easily be removed, but is retained so that overloading
# is possible in the Java code.
# I is integer, V is void.  The last type in the name is the return type.

= (test1 mult-I-I-I 15 10) 150;

# The type information can be safely omitted if there is no ambiguity

= (test1 mult 15 10) 150;

= (test1 addmult-I-I-I-I 4 15 10) 154;

begin
  (test1 set-I-V 87)
  (= (test1 get-I) 87);

= (test1 fact-I-I 0) 1;

= (test1 fact-I-I 1) 1;

= (test1 fact-I-I 5) 120;

# Yay! testing says this works.
# So structure for bytecode interpretation is in place.
# Very few opcodes actually implemented yet though.

56. another simple little text-adventure space

# let us try to make a slightly more interesting world

define make-table
  (lambda (lst)
    (crunch (? x / ? h / 
           assign name (car / x) /
           assign obj (cdr / x) /
           hash-add (h) (name) (obj))
        (append (hash-null) (lst))));

# note, the quoted strings below are just represented as a big number,
# nothing special

define geo-map 
  (make-table
   (map
    (? name (cons (name) (room new (name))))
    (vector "boston" "dublin" "paris" "genoa")));

define my-links
  (map 
   (? entry (assign src (car / entry) /
            assign dest (cdr / entry) /
            door new (geo-map / src) (geo-map / dest)))
   (vector
    (cons "boston" "dublin")
    (cons "dublin" "paris")
    (cons "boston" "paris")
    (cons "paris" "genoa")));

define myrobo (robo new);

myrobo set-room (geo-map "dublin");

(equal "dublin" / myrobo get-room name);

myrobo update;

(equal "paris" / myrobo get-room name);

myrobo update;

(equal "genoa" / myrobo get-room name);

myrobo update;

(equal "paris" / myrobo get-room name);

myrobo update;

(equal "boston" / myrobo get-room name);

myrobo update;

(equal "dublin" / myrobo get-room name);

myrobo update;

(equal "paris" / myrobo get-room name);

# all characters should update together

class world (the-places the-links)
       (field things (container new))
       (field names (cell new (hash-null)))
       (field places (cell new 0))
       (field links (cell new 0))
       (method new 
           (begin
         (places set
            (make-table
             (map
              (? name (cons (name) (room new (name))))
              (the-places))))
         (links set
            (map 
             (? entry (assign src (car / entry) /
                      assign dest (cdr / entry) /
                      door new 
                      (places get / src) 
                      (places get / dest)))
             (the-links)))))
       (method add (lambda (place name val) 
             (begin
               (val set-room (places get / place))
               (val set-name / name)
               (names set (hash-add (names get)
                        (name)
                        (val)))
               (things add (val)))))
       (method find (lambda (n) (names get (n) get-room name)))
       (method reachable (lambda (place)
               (let ((exits
                  (select-match (lambda (x) 
                          (instanceof door (x)))
                        (places get (place) inventory))))
                 (map (? door (door access-from 
                        (places get / place)
                        name))
                  (exits)))))
       (method update (begin 
            (map (? x (x update)) 
                 (things inventory))
            (true)));

define geo-world
  (world new 
     (vector "boston" "dublin" "paris" "genoa")
     (vector
      (cons "boston" "dublin")
      (cons "dublin" "paris")
      (cons "boston" "paris")
      (cons "paris" "genoa")));

geo-world add "dublin" "robo1" (robo new);

geo-world add "genoa" "robo2" (robo new);

(equal "dublin" / geo-world find "robo1");

(equal "genoa" / geo-world find "robo2");

geo-world update;

(equal "paris" / geo-world find "robo1");

(equal "paris" / geo-world find "robo2");

(equal (vector "paris" "dublin") / geo-world reachable "boston");

(equal (vector "paris") / geo-world reachable "genoa");

57. native implementation of a Java list, hash classes

define flex-equals
  (lambda (x y) 
    (if (number? / x)
    (if (number? / y)
        (= (x) (y))
        (false))
    (if (number? / y)
        (false)
        (x equals (y)))));

define remove-object
  (lambda (x) 
    (remove-match (lambda (y) 
            (flex-equals (x) (y)))));

define contains-object
  (lambda (x lst)
    (if (> (list-length / lst) 0)
    (if (flex-equals (head / lst) (x))
        (true)
        (contains-object (x) (tail / lst)))
    (false)));

class COS_JList ()
       (field super ((java lang Object) new))
       (method unknown (lambda (x) (super (x))))
       (field contents (cell new (vector)))
       (method <init>-V (self))
       (method <init> (self <init>-V))
       (method add-Object-V (lambda (x)
             (contents set (prepend (x) (contents get)))))
       (method add (self add-Object-V))
       (method remove-Object-Z (lambda (x)
            (contents set 
                  (remove-object (x) (contents get)))))
       (method remove (self remove-Object-Z))
       (method contains-Object-Z (lambda (x)
                   (contains-object (x) (contents get))))
       (method contains (self contains-Object-Z))
       (method get-I-Object (lambda (x)
             (list-ref (contents get) (x))))
       (method get (self get-I-Object))
       (method iterator-Iterator (COS_JListIterator new (self)))
       (method iterator (self iterator-Iterator))
       (method size-V-I (list-length (contents get)))
       (method size (self size-V-I));

define test1 (COS_JList new);

begin (test1 add-Object-V (test1))
       (= 1 / test1 size-V-I);

test1 == (test1 get-I-Object 0);

class COS_JHashMap ()
       (field super ((java lang Object) new))
       (method unknown (lambda (x) (super (x))))
       (field contents (cell new (? x 0)))
       (method <init>-V (self))
       (method <init> (self <init>-V))
       (method put-Object-Object-V (lambda (x y)
                     (let ((prev / contents get))
                       (contents set 
                         (? z 
                            (if (flex-equals (z) (x))
                            (y)
                            (prev (z))))))))
       (method put (self put-Object-Object-V))
       (method get-Object-Object (lambda (x)
                   (contents get (x))))
       (method get (self get-Object-Object));

define test2 (COS_JHashMap new);

begin (test2 put-Object-Object-V 5 10)
       (= 10 / test2 get 5);

# There is Java code for COS_JList available

# There is Java code for COS_JHashMap available

58. testing the JList class

define test1 (COS_JList new);

begin (test1 add-Object-V (test1))
       (= 1 (test1 size-V-I));

(test1 get-I-Object 0) == (test1);

59. basic iterator implementation

class COS_JListIterator (ref)
       (field pipe (cell new (ref contents get)))
       (method <init>-V (self))
       (method <init> (self <init>-V))
       (method hasNext-Z (> (list-length / pipe get) 0))
       (method hasNext (self hasNext-Z))
       (method next (self next-Object))
       (method next-Object 
           (let ((result (head / pipe get)))
         (begin 
           (pipe set / tail / pipe get)
           (result))));

define test1 (COS_JList new);

begin
  (test1 add 15)
  (test1 add 72)
  (test1 add 99)
  (true);

define iter1 (test1 iterator);

iter1 hasNext;

(equal 99 / iter1 next);

iter1 hasNext;

(equal 72 / iter1 next);

iter1 hasNext;

(equal 15 / iter1 next);

not / iter1 hasNext;

# There is Java code for COS_JListIterator available

60. class translation 'COS_JDoor'

# Sun Mar 23 02:45:10 CET 2014
# Produced by Fritzifier, based on JasminVisitor
# Using BCEL library to read Java bytecode
# Here is the original code:
# 
# public class COS_JDoor {
#     private COS_JRoom src, dest;
#     private String src_cmd, dest_cmd;
# 
#     public COS_JDoor(COS_JRoom src, String src_cmd,
#              COS_JRoom dest, String dest_cmd) {
#     this.src = src;
#     this.dest = dest;
#     this.src_cmd = src_cmd;
#     this.dest_cmd = dest_cmd;
#     src.addDoor(this);
#     dest.addDoor(this);
#     }
# 
#     public COS_JRoom apply(COS_JRoom src, String cmd) {
#     if (src == this.src) {
#         if (src_cmd.equals(cmd)) {
#         return this.dest;
#         }
#     }
#     if (src == this.dest) {
#         if (dest_cmd.equals(cmd)) {
#         return this.src;
#         }
#     }
#     return null;
#     }
# 
#     public COS_JRoom apply(COS_JRoom src) {
#     if (src==this.src) {
#         return this.dest;
#     }
#     if (src==this.dest) {
#         return this.src;
#     }
#     return null;
#     }
# }

class COS_JDoor ()
   (field super-ref (make-cell 0))
   (method new (set! (super-ref) ((java lang Object) / this)))
   (method super (? x / (get! / super-ref) / x))
   (method unknown (? x / self super / x))
   (field src (cell new 0))
   (field dest (cell new 0))
   (field src_cmd (cell new 0))
   (field dest_cmd (cell new 0))
   (method <init>-COS_JRoom-String-COS_JRoom-String-V
     (lambda (arg0 arg1 arg2 arg3) /
      let ((vars / cell new / make-hash / vector
                    (pair 0 (self)) (pair 1 (arg0)) (pair 2 (arg1)) (pair 3 (arg2)) (pair 4 (arg3)))
           (stack / cell new / vector)) /
      state-machine (vars) (stack) / ? jvm / ? x / cond
         ((= (x) 0) (jvm aload 0))
         ((= (x) 1) (jvm invokespecial <init>-V 0 0))
         ((= (x) 2) (jvm aload 0))
         ((= (x) 3) (jvm aload 1))
         ((= (x) 4) (jvm putfield src (COS_JRoom)))
         ((= (x) 5) (jvm aload 0))
         ((= (x) 6) (jvm aload 3))
         ((= (x) 7) (jvm putfield dest (COS_JRoom)))
         ((= (x) 8) (jvm aload 0))
         ((= (x) 9) (jvm aload 2))
         ((= (x) 10) (jvm putfield src_cmd (java lang String)))
         ((= (x) 11) (jvm aload 0))
         ((= (x) 12) (jvm aload 4))
         ((= (x) 13) (jvm putfield dest_cmd (java lang String)))
         ((= (x) 14) (jvm aload 1))
         ((= (x) 15) (jvm aload 0))
         ((= (x) 16) (jvm invokevirtual addDoor-COS_JDoor-V 1 0))
         ((= (x) 17) (jvm aload 3))
         ((= (x) 18) (jvm aload 0))
         ((= (x) 19) (jvm invokevirtual addDoor-COS_JDoor-V 1 0))
         ((= (x) 20) (jvm return))
         (jvm return))
   )

   (method <init> (self <init>-COS_JRoom-String-COS_JRoom-String-V))

   (method apply-COS_JRoom-String-COS_JRoom
     (lambda (arg0 arg1) /
      let ((vars / cell new / make-hash / vector
                    (pair 0 (self)) (pair 1 (arg0)) (pair 2 (arg1)))
           (stack / cell new / vector)) /
      state-machine (vars) (stack) / ? jvm / ? x / cond
         ((= (x) 0) (jvm aload 1))
         ((= (x) 1) (jvm aload 0))
         ((= (x) 2) (jvm getfield src (COS_JRoom)))
         ((= (x) 3) (jvm if_acmpne 12))
         ((= (x) 4) (jvm aload 0))
         ((= (x) 5) (jvm getfield src_cmd (java lang String)))
         ((= (x) 6) (jvm aload 2))
         ((= (x) 7) (jvm invokevirtual equals-Object-Z 1 1))
         ((= (x) 8) (jvm ifeq 12))
         ((= (x) 9) (jvm aload 0))
         ((= (x) 10) (jvm getfield dest (COS_JRoom)))
         ((= (x) 11) (jvm areturn))
         ((= (x) 12) (jvm aload 1))
         ((= (x) 13) (jvm aload 0))
         ((= (x) 14) (jvm getfield dest (COS_JRoom)))
         ((= (x) 15) (jvm if_acmpne 24))
         ((= (x) 16) (jvm aload 0))
         ((= (x) 17) (jvm getfield dest_cmd (java lang String)))
         ((= (x) 18) (jvm aload 2))
         ((= (x) 19) (jvm invokevirtual equals-Object-Z 1 1))
         ((= (x) 20) (jvm ifeq 24))
         ((= (x) 21) (jvm aload 0))
         ((= (x) 22) (jvm getfield src (COS_JRoom)))
         ((= (x) 23) (jvm areturn))
         ((= (x) 24) (jvm aconst_null))
         ((= (x) 25) (jvm areturn))
         (jvm return))
   )

   (method apply (self apply-COS_JRoom-String-COS_JRoom))

   (method apply-COS_JRoom-COS_JRoom
     (lambda (arg0) /
      let ((vars / cell new / make-hash / vector
                    (pair 0 (self)) (pair 1 (arg0)))
           (stack / cell new / vector)) /
      state-machine (vars) (stack) / ? jvm / ? x / cond
         ((= (x) 0) (jvm aload 1))
         ((= (x) 1) (jvm aload 0))
         ((= (x) 2) (jvm getfield src (COS_JRoom)))
         ((= (x) 3) (jvm if_acmpne 7))
         ((= (x) 4) (jvm aload 0))
         ((= (x) 5) (jvm getfield dest (COS_JRoom)))
         ((= (x) 6) (jvm areturn))
         ((= (x) 7) (jvm aload 1))
         ((= (x) 8) (jvm aload 0))
         ((= (x) 9) (jvm getfield dest (COS_JRoom)))
         ((= (x) 10) (jvm if_acmpne 14))
         ((= (x) 11) (jvm aload 0))
         ((= (x) 12) (jvm getfield src (COS_JRoom)))
         ((= (x) 13) (jvm areturn))
         ((= (x) 14) (jvm aconst_null))
         ((= (x) 15) (jvm areturn))
         (jvm return))
   )

 ;

61. class translation 'COS_JThing'

# Sun Mar 23 02:45:11 CET 2014
# Produced by Fritzifier, based on JasminVisitor
# Using BCEL library to read Java bytecode
# Here is the original code:
# 
# public class COS_JThing extends COS_JNamed {
#     private COS_JRoom location;
#     private COS_JRoom nextLocation;
# 
#     public void setRoom(COS_JRoom location) {
#     if (this.location!=null) {
#         this.location.removeThing(this);
#     }
#     this.location = location;
#     location.addThing(this);
#     this.nextLocation = location;
#     }
#     
#     public COS_JRoom getRoom() {
#     return location;
#     }
# 
#     public void setNextRoom(COS_JRoom location) {
#     nextLocation = location;
#     }
# 
#     public void postUpdate() {
#     if (nextLocation!=location) {
#         setRoom(nextLocation);
#     }
#     }
# }
# 

class COS_JThing ()
   (field super-ref (make-cell 0))
   (method new (set! (super-ref) ((COS_JNamed) / this)))
   (method super (? x / (get! / super-ref) / x))
   (method unknown (? x / self super / x))
   (field location (cell new 0))
   (field nextLocation (cell new 0))
   (method <init>-V
     (lambda () /
      let ((vars / cell new / make-hash / vector
                    (pair 0 (self)))
           (stack / cell new / vector)) /
      state-machine (vars) (stack) / ? jvm / ? x / cond
         ((= (x) 0) (jvm aload 0))
         ((= (x) 1) (jvm invokespecial <init>-V 0 0))
         ((= (x) 2) (jvm return))
         (jvm return))
   )

   (method <init> (self <init>-V))

   (method setRoom-COS_JRoom-V
     (lambda (arg0) /
      let ((vars / cell new / make-hash / vector
                    (pair 0 (self)) (pair 1 (arg0)))
           (stack / cell new / vector)) /
      state-machine (vars) (stack) / ? jvm / ? x / cond
         ((= (x) 0) (jvm aload 0))
         ((= (x) 1) (jvm getfield location (COS_JRoom)))
         ((= (x) 2) (jvm ifnull 7))
         ((= (x) 3) (jvm aload 0))
         ((= (x) 4) (jvm getfield location (COS_JRoom)))
         ((= (x) 5) (jvm aload 0))
         ((= (x) 6) (jvm invokevirtual removeThing-COS_JThing-V 1 0))
         ((= (x) 7) (jvm aload 0))
         ((= (x) 8) (jvm aload 1))
         ((= (x) 9) (jvm putfield location (COS_JRoom)))
         ((= (x) 10) (jvm aload 1))
         ((= (x) 11) (jvm aload 0))
         ((= (x) 12) (jvm invokevirtual addThing-COS_JThing-V 1 0))
         ((= (x) 13) (jvm aload 0))
         ((= (x) 14) (jvm aload 1))
         ((= (x) 15) (jvm putfield nextLocation (COS_JRoom)))
         ((= (x) 16) (jvm return))
         (jvm return))
   )

   (method setRoom (self setRoom-COS_JRoom-V))

   (method getRoom-COS_JRoom
     (lambda () /
      let ((vars / cell new / make-hash / vector
                    (pair 0 (self)))
           (stack / cell new / vector)) /
      state-machine (vars) (stack) / ? jvm / ? x / cond
         ((= (x) 0) (jvm aload 0))
         ((= (x) 1) (jvm getfield location (COS_JRoom)))
         ((= (x) 2) (jvm areturn))
         (jvm return))
   )

   (method getRoom (self getRoom-COS_JRoom))

   (method setNextRoom-COS_JRoom-V
     (lambda (arg0) /
      let ((vars / cell new / make-hash / vector
                    (pair 0 (self)) (pair 1 (arg0)))
           (stack / cell new / vector)) /
      state-machine (vars) (stack) / ? jvm / ? x / cond
         ((= (x) 0) (jvm aload 0))
         ((= (x) 1) (jvm aload 1))
         ((= (x) 2) (jvm putfield nextLocation (COS_JRoom)))
         ((= (x) 3) (jvm return))
         (jvm return))
   )

   (method setNextRoom (self setNextRoom-COS_JRoom-V))

   (method postUpdate-V
     (lambda () /
      let ((vars / cell new / make-hash / vector
                    (pair 0 (self)))
           (stack / cell new / vector)) /
      state-machine (vars) (stack) / ? jvm / ? x / cond
         ((= (x) 0) (jvm aload 0))
         ((= (x) 1) (jvm getfield nextLocation (COS_JRoom)))
         ((= (x) 2) (jvm aload 0))
         ((= (x) 3) (jvm getfield location (COS_JRoom)))
         ((= (x) 4) (jvm if_acmpeq 9))
         ((= (x) 5) (jvm aload 0))
         ((= (x) 6) (jvm aload 0))
         ((= (x) 7) (jvm getfield nextLocation (COS_JRoom)))
         ((= (x) 8) (jvm invokevirtual setRoom-COS_JRoom-V 1 0))
         ((= (x) 9) (jvm return))
         (jvm return))
   )

   (method postUpdate (self postUpdate-V))

 ;

62. class translation 'COS_JRoom'

# Sun Mar 23 02:45:12 CET 2014
# Produced by Fritzifier, based on JasminVisitor
# Using BCEL library to read Java bytecode
# Here is the original code:
# 
# import java.util.Iterator;
# 
# public class COS_JRoom extends COS_JNamed {
#     //private COS_JList content = new COS_JList();
#     //private COS_JList doors = new COS_JList();
# 
#     private COS_JList content;
#     private COS_JList doors;
# 
#     public COS_JRoom() {
#     content = new COS_JList();
#     doors = new COS_JList();
#     }
# 
#     public COS_JList get() {
#     return content;
#     }
# 
#     public Iterator getDoors() {
#     return doors.iterator();
#     }
# 
#     public void addDoor(COS_JDoor door) {
#     //System.out.println("add door -> " + getName());
#     doors.add(door);
#     }
# 
#     public void addThing(COS_JThing thing) {
#     content.add(thing);
#     }
# 
#     public void removeThing(COS_JThing thing) {
#     content.remove(thing);
#     }
# }

class COS_JRoom ()
   (field super-ref (make-cell 0))
   (method new (set! (super-ref) ((COS_JNamed) / this)))
   (method super (? x / (get! / super-ref) / x))
   (method unknown (? x / self super / x))
   (field content (cell new 0))
   (field doors (cell new 0))
   (method <init>-V
     (lambda () /
      let ((vars / cell new / make-hash / vector
                    (pair 0 (self)))
           (stack / cell new / vector)) /
      state-machine (vars) (stack) / ? jvm / ? x / cond
         ((= (x) 0) (jvm aload 0))
         ((= (x) 1) (jvm invokespecial <init>-V 0 0))
         ((= (x) 2) (jvm aload 0))
         ((= (x) 3) (jvm new (COS_JList)))
         ((= (x) 4) (jvm dup))
         ((= (x) 5) (jvm invokespecial <init>-V 0 0))
         ((= (x) 6) (jvm putfield content (COS_JList)))
         ((= (x) 7) (jvm aload 0))
         ((= (x) 8) (jvm new (COS_JList)))
         ((= (x) 9) (jvm dup))
         ((= (x) 10) (jvm invokespecial <init>-V 0 0))
         ((= (x) 11) (jvm putfield doors (COS_JList)))
         ((= (x) 12) (jvm return))
         (jvm return))
   )

   (method <init> (self <init>-V))

   (method get-COS_JList
     (lambda () /
      let ((vars / cell new / make-hash / vector
                    (pair 0 (self)))
           (stack / cell new / vector)) /
      state-machine (vars) (stack) / ? jvm / ? x / cond
         ((= (x) 0) (jvm aload 0))
         ((= (x) 1) (jvm getfield content (COS_JList)))
         ((= (x) 2) (jvm areturn))
         (jvm return))
   )

   (method get (self get-COS_JList))

   (method getDoors-Iterator
     (lambda () /
      let ((vars / cell new / make-hash / vector
                    (pair 0 (self)))
           (stack / cell new / vector)) /
      state-machine (vars) (stack) / ? jvm / ? x / cond
         ((= (x) 0) (jvm aload 0))
         ((= (x) 1) (jvm getfield doors (COS_JList)))
         ((= (x) 2) (jvm invokevirtual iterator-Iterator 0 1))
         ((= (x) 3) (jvm areturn))
         (jvm return))
   )

   (method getDoors (self getDoors-Iterator))

   (method addDoor-COS_JDoor-V
     (lambda (arg0) /
      let ((vars / cell new / make-hash / vector
                    (pair 0 (self)) (pair 1 (arg0)))
           (stack / cell new / vector)) /
      state-machine (vars) (stack) / ? jvm / ? x / cond
         ((= (x) 0) (jvm aload 0))
         ((= (x) 1) (jvm getfield doors (COS_JList)))
         ((= (x) 2) (jvm aload 1))
         ((= (x) 3) (jvm invokevirtual add-Object-V 1 0))
         ((= (x) 4) (jvm return))
         (jvm return))
   )

   (method addDoor (self addDoor-COS_JDoor-V))

   (method addThing-COS_JThing-V
     (lambda (arg0) /
      let ((vars / cell new / make-hash / vector
                    (pair 0 (self)) (pair 1 (arg0)))
           (stack / cell new / vector)) /
      state-machine (vars) (stack) / ? jvm / ? x / cond
         ((= (x) 0) (jvm aload 0))
         ((= (x) 1) (jvm getfield content (COS_JList)))
         ((= (x) 2) (jvm aload 1))
         ((= (x) 3) (jvm invokevirtual add-Object-V 1 0))
         ((= (x) 4) (jvm return))
         (jvm return))
   )

   (method addThing (self addThing-COS_JThing-V))

   (method removeThing-COS_JThing-V
     (lambda (arg0) /
      let ((vars / cell new / make-hash / vector
                    (pair 0 (self)) (pair 1 (arg0)))
           (stack / cell new / vector)) /
      state-machine (vars) (stack) / ? jvm / ? x / cond
         ((= (x) 0) (jvm aload 0))
         ((= (x) 1) (jvm getfield content (COS_JList)))
         ((= (x) 2) (jvm aload 1))
         ((= (x) 3) (jvm invokevirtual remove-Object-Z 1 1))
         ((= (x) 4) (jvm pop))
         ((= (x) 5) (jvm return))
         (jvm return))
   )

   (method removeThing (self removeThing-COS_JThing-V))

 ;

63. class translation 'COS_JNamed'

# Sun Mar 23 02:45:13 CET 2014
# Produced by Fritzifier, based on JasminVisitor
# Using BCEL library to read Java bytecode
# Here is the original code:
# 
# public class COS_JNamed {
#     private String name = "-";
#     private COS_JWorld world = null;
# 
#     void setName(String name) {
#     this.name = name;
#     }
# 
#     String getName() {
#     return name;
#     }
# 
#     void setWorld(COS_JWorld world) {
#     this.world = world;
#     }
# 
#     COS_JWorld getWorld() {
#     return world;
#     }
# 
#     void update() {
#     }
# 
#     void postUpdate() {
#     }
# }

class COS_JNamed ()
   (field super-ref (make-cell 0))
   (method new (set! (super-ref) ((java lang Object) / this)))
   (method super (? x / (get! / super-ref) / x))
   (method unknown (? x / self super / x))
   (field name (cell new 0))
   (field world (cell new 0))
   (method <init>-V
     (lambda () /
      let ((vars / cell new / make-hash / vector
                    (pair 0 (self)))
           (stack / cell new / vector)) /
      state-machine (vars) (stack) / ? jvm / ? x / cond
         ((= (x) 0) (jvm aload 0))
         ((= (x) 1) (jvm invokespecial <init>-V 0 0))
         ((= (x) 2) (jvm aload 0))
         ((= (x) 3) (jvm ldc (String new int-init "-")))
         ((= (x) 4) (jvm putfield name (java lang String)))
         ((= (x) 5) (jvm aload 0))
         ((= (x) 6) (jvm aconst_null))
         ((= (x) 7) (jvm putfield world (COS_JWorld)))
         ((= (x) 8) (jvm return))
         (jvm return))
   )

   (method <init> (self <init>-V))

   (method setName-String-V
     (lambda (arg0) /
      let ((vars / cell new / make-hash / vector
                    (pair 0 (self)) (pair 1 (arg0)))
           (stack / cell new / vector)) /
      state-machine (vars) (stack) / ? jvm / ? x / cond
         ((= (x) 0) (jvm aload 0))
         ((= (x) 1) (jvm aload 1))
         ((= (x) 2) (jvm putfield name (java lang String)))
         ((= (x) 3) (jvm return))
         (jvm return))
   )

   (method setName (self setName-String-V))

   (method getName-String
     (lambda () /
      let ((vars / cell new / make-hash / vector
                    (pair 0 (self)))
           (stack / cell new / vector)) /
      state-machine (vars) (stack) / ? jvm / ? x / cond
         ((= (x) 0) (jvm aload 0))
         ((= (x) 1) (jvm getfield name (java lang String)))
         ((= (x) 2) (jvm areturn))
         (jvm return))
   )

   (method getName (self getName-String))

   (method setWorld-COS_JWorld-V
     (lambda (arg0) /
      let ((vars / cell new / make-hash / vector
                    (pair 0 (self)) (pair 1 (arg0)))
           (stack / cell new / vector)) /
      state-machine (vars) (stack) / ? jvm / ? x / cond
         ((= (x) 0) (jvm aload 0))
         ((= (x) 1) (jvm aload 1))
         ((= (x) 2) (jvm putfield world (COS_JWorld)))
         ((= (x) 3) (jvm return))
         (jvm return))
   )

   (method setWorld (self setWorld-COS_JWorld-V))

   (method getWorld-COS_JWorld
     (lambda () /
      let ((vars / cell new / make-hash / vector
                    (pair 0 (self)))
           (stack / cell new / vector)) /
      state-machine (vars) (stack) / ? jvm / ? x / cond
         ((= (x) 0) (jvm aload 0))
         ((= (x) 1) (jvm getfield world (COS_JWorld)))
         ((= (x) 2) (jvm areturn))
         (jvm return))
   )

   (method getWorld (self getWorld-COS_JWorld))

   (method update-V
     (lambda () /
      let ((vars / cell new / make-hash / vector
                    (pair 0 (self)))
           (stack / cell new / vector)) /
      state-machine (vars) (stack) / ? jvm / ? x / cond
         ((= (x) 0) (jvm return))
         (jvm return))
   )

   (method update (self update-V))

   (method postUpdate-V
     (lambda () /
      let ((vars / cell new / make-hash / vector
                    (pair 0 (self)))
           (stack / cell new / vector)) /
      state-machine (vars) (stack) / ? jvm / ? x / cond
         ((= (x) 0) (jvm return))
         (jvm return))
   )

   (method postUpdate (self postUpdate-V))

 ;

64. class translation 'COS_JWorld'

# Sun Mar 23 02:45:14 CET 2014
# Produced by Fritzifier, based on JasminVisitor
# Using BCEL library to read Java bytecode
# Here is the original code:
# 
# import java.util.Iterator;
# 
# public class COS_JWorld {
#     private COS_JHashMap content;
#     private COS_JList inventory;
# 
#     public COS_JWorld() {
#     content = new COS_JHashMap();
#     inventory = new COS_JList();
#     }
# 
#     public void add(COS_JNamed named, String name) {
#     named.setName(name);
#     content.put(named.getName(),named);
#     inventory.add(named);
#     }
# 
#     public COS_JNamed get(String name) {
#     return (COS_JNamed)content.get(new String(name));
#     }
# 
#     public void update() {
#     for (Iterator i = inventory.iterator(); i.hasNext(); ) {
#         COS_JNamed o = (COS_JNamed) i.next();
#         o.update();
#     }
#     for (Iterator i = inventory.iterator(); i.hasNext(); ) {
#         COS_JNamed o = (COS_JNamed) i.next();
#         o.postUpdate();
#     }
#     }
# }

class COS_JWorld ()
   (field super-ref (make-cell 0))
   (method new (set! (super-ref) ((java lang Object) / this)))
   (method super (? x / (get! / super-ref) / x))
   (method unknown (? x / self super / x))
   (field content (cell new 0))
   (field inventory (cell new 0))
   (method <init>-V
     (lambda () /
      let ((vars / cell new / make-hash / vector
                    (pair 0 (self)))
           (stack / cell new / vector)) /
      state-machine (vars) (stack) / ? jvm / ? x / cond
         ((= (x) 0) (jvm aload 0))
         ((= (x) 1) (jvm invokespecial <init>-V 0 0))
         ((= (x) 2) (jvm aload 0))
         ((= (x) 3) (jvm new (COS_JHashMap)))
         ((= (x) 4) (jvm dup))
         ((= (x) 5) (jvm invokespecial <init>-V 0 0))
         ((= (x) 6) (jvm putfield content (COS_JHashMap)))
         ((= (x) 7) (jvm aload 0))
         ((= (x) 8) (jvm new (COS_JList)))
         ((= (x) 9) (jvm dup))
         ((= (x) 10) (jvm invokespecial <init>-V 0 0))
         ((= (x) 11) (jvm putfield inventory (COS_JList)))
         ((= (x) 12) (jvm return))
         (jvm return))
   )

   (method <init> (self <init>-V))

   (method add-COS_JNamed-String-V
     (lambda (arg0 arg1) /
      let ((vars / cell new / make-hash / vector
                    (pair 0 (self)) (pair 1 (arg0)) (pair 2 (arg1)))
           (stack / cell new / vector)) /
      state-machine (vars) (stack) / ? jvm / ? x / cond
         ((= (x) 0) (jvm aload 1))
         ((= (x) 1) (jvm aload 2))
         ((= (x) 2) (jvm invokevirtual setName-String-V 1 0))
         ((= (x) 3) (jvm aload 0))
         ((= (x) 4) (jvm getfield content (COS_JHashMap)))
         ((= (x) 5) (jvm aload 1))
         ((= (x) 6) (jvm invokevirtual getName-String 0 1))
         ((= (x) 7) (jvm aload 1))
         ((= (x) 8) (jvm invokevirtual put-Object-Object-V 2 0))
         ((= (x) 9) (jvm aload 0))
         ((= (x) 10) (jvm getfield inventory (COS_JList)))
         ((= (x) 11) (jvm aload 1))
         ((= (x) 12) (jvm invokevirtual add-Object-V 1 0))
         ((= (x) 13) (jvm return))
         (jvm return))
   )

   (method add (self add-COS_JNamed-String-V))

   (method get-String-COS_JNamed
     (lambda (arg0) /
      let ((vars / cell new / make-hash / vector
                    (pair 0 (self)) (pair 1 (arg0)))
           (stack / cell new / vector)) /
      state-machine (vars) (stack) / ? jvm / ? x / cond
         ((= (x) 0) (jvm aload 0))
         ((= (x) 1) (jvm getfield content (COS_JHashMap)))
         ((= (x) 2) (jvm new (java lang String)))
         ((= (x) 3) (jvm dup))
         ((= (x) 4) (jvm aload 1))
         ((= (x) 5) (jvm invokespecial <init>-String-V 1 0))
         ((= (x) 6) (jvm invokevirtual get-Object-Object 1 1))
         ((= (x) 7) (jvm checkcast (COS_JNamed)))
         ((= (x) 8) (jvm areturn))
         (jvm return))
   )

   (method get (self get-String-COS_JNamed))

   (method update-V
     (lambda () /
      let ((vars / cell new / make-hash / vector
                    (pair 0 (self)))
           (stack / cell new / vector)) /
      state-machine (vars) (stack) / ? jvm / ? x / cond
         ((= (x) 0) (jvm aload 0))
         ((= (x) 1) (jvm getfield inventory (COS_JList)))
         ((= (x) 2) (jvm invokevirtual iterator-Iterator 0 1))
         ((= (x) 3) (jvm astore 1))
         ((= (x) 4) (jvm aload 1))
         ((= (x) 5) (jvm invokeinterface hasNext-Z 0 1 1))
         ((= (x) 6) (jvm ifeq 14))
         ((= (x) 7) (jvm aload 1))
         ((= (x) 8) (jvm invokeinterface next-Object 0 1 1))
         ((= (x) 9) (jvm checkcast (COS_JNamed)))
         ((= (x) 10) (jvm astore 2))
         ((= (x) 11) (jvm aload 2))
         ((= (x) 12) (jvm invokevirtual update-V 0 0))
         ((= (x) 13) (jvm goto 4))
         ((= (x) 14) (jvm aload 0))
         ((= (x) 15) (jvm getfield inventory (COS_JList)))
         ((= (x) 16) (jvm invokevirtual iterator-Iterator 0 1))
         ((= (x) 17) (jvm astore 1))
         ((= (x) 18) (jvm aload 1))
         ((= (x) 19) (jvm invokeinterface hasNext-Z 0 1 1))
         ((= (x) 20) (jvm ifeq 28))
         ((= (x) 21) (jvm aload 1))
         ((= (x) 22) (jvm invokeinterface next-Object 0 1 1))
         ((= (x) 23) (jvm checkcast (COS_JNamed)))
         ((= (x) 24) (jvm astore 2))
         ((= (x) 25) (jvm aload 2))
         ((= (x) 26) (jvm invokevirtual postUpdate-V 0 0))
         ((= (x) 27) (jvm goto 18))
         ((= (x) 28) (jvm return))
         (jvm return))
   )

   (method update (self update-V))

 ;

65. class translation 'COS_JRobo'

# Sun Mar 23 02:45:16 CET 2014
# Produced by Fritzifier, based on JasminVisitor
# Using BCEL library to read Java bytecode
# Here is the original code:
# 
# import java.util.Iterator;
# 
# public class COS_JRobo extends COS_JThing {
#     private COS_JHashMap times;
#     private int now;
# 
#     public COS_JRobo() {
#     times = new COS_JHashMap();
#     now = 1;
#     }
# 
#     public void update() {
#     COS_JRoom location = getRoom();
#     //System.out.println("Updating robo...");
#     if (location!=null) {
#         int oldestTime = now;
#         COS_JDoor oldestDoor = null;
#         for (Iterator i = location.getDoors(); i.hasNext(); ) {
#         COS_JDoor door = (COS_JDoor) i.next();
#         //System.out.println(" scanning door ");
#         Integer t = (Integer)times.get(door);
#         int v = 0;
#         if (t!=null) {
#             v = t.intValue();
#         }
#         if (v<oldestTime) {
#             oldestTime = v;
#             oldestDoor = door;
#         }
#         }
#         if (oldestDoor!=null) {
#         times.put(oldestDoor,new Integer(now));
#         setNextRoom(oldestDoor.apply(location));
#         }
#     }
#     now++;
#     }
# }
# 

class COS_JRobo ()
   (field super-ref (make-cell 0))
   (method new (set! (super-ref) ((COS_JThing) / this)))
   (method super (? x / (get! / super-ref) / x))
   (method unknown (? x / self super / x))
   (field times (cell new 0))
   (field now ((int) new))
   (method <init>-V
     (lambda () /
      let ((vars / cell new / make-hash / vector
                    (pair 0 (self)))
           (stack / cell new / vector)) /
      state-machine (vars) (stack) / ? jvm / ? x / cond
         ((= (x) 0) (jvm aload 0))
         ((= (x) 1) (jvm invokespecial <init>-V 0 0))
         ((= (x) 2) (jvm aload 0))
         ((= (x) 3) (jvm new (COS_JHashMap)))
         ((= (x) 4) (jvm dup))
         ((= (x) 5) (jvm invokespecial <init>-V 0 0))
         ((= (x) 6) (jvm putfield times (COS_JHashMap)))
         ((= (x) 7) (jvm aload 0))
         ((= (x) 8) (jvm iconst 1))
         ((= (x) 9) (jvm putfield now (int)))
         ((= (x) 10) (jvm return))
         (jvm return))
   )

   (method <init> (self <init>-V))

   (method update-V
     (lambda () /
      let ((vars / cell new / make-hash / vector
                    (pair 0 (self)))
           (stack / cell new / vector)) /
      state-machine (vars) (stack) / ? jvm / ? x / cond
         ((= (x) 0) (jvm aload 0))
         ((= (x) 1) (jvm invokevirtual getRoom-COS_JRoom 0 1))
         ((= (x) 2) (jvm astore 1))
         ((= (x) 3) (jvm aload 1))
         ((= (x) 4) (jvm ifnull 57))
         ((= (x) 5) (jvm aload 0))
         ((= (x) 6) (jvm getfield now (int)))
         ((= (x) 7) (jvm istore 2))
         ((= (x) 8) (jvm aconst_null))
         ((= (x) 9) (jvm astore 3))
         ((= (x) 10) (jvm aload 1))
         ((= (x) 11) (jvm invokevirtual getDoors-Iterator 0 1))
         ((= (x) 12) (jvm astore 4))
         ((= (x) 13) (jvm aload 4))
         ((= (x) 14) (jvm invokeinterface hasNext-Z 0 1 1))
         ((= (x) 15) (jvm ifeq 41))
         ((= (x) 16) (jvm aload 4))
         ((= (x) 17) (jvm invokeinterface next-Object 0 1 1))
         ((= (x) 18) (jvm checkcast (COS_JDoor)))
         ((= (x) 19) (jvm astore 5))
         ((= (x) 20) (jvm aload 0))
         ((= (x) 21) (jvm getfield times (COS_JHashMap)))
         ((= (x) 22) (jvm aload 5))
         ((= (x) 23) (jvm invokevirtual get-Object-Object 1 1))
         ((= (x) 24) (jvm checkcast (java lang Integer)))
         ((= (x) 25) (jvm astore 6))
         ((= (x) 26) (jvm iconst 0))
         ((= (x) 27) (jvm istore 7))
         ((= (x) 28) (jvm aload 6))
         ((= (x) 29) (jvm ifnull 33))
         ((= (x) 30) (jvm aload 6))
         ((= (x) 31) (jvm invokevirtual intValue-I 0 1))
         ((= (x) 32) (jvm istore 7))
         ((= (x) 33) (jvm iload 7))
         ((= (x) 34) (jvm iload 2))
         ((= (x) 35) (jvm if_icmpge 40))
         ((= (x) 36) (jvm iload 7))
         ((= (x) 37) (jvm istore 2))
         ((= (x) 38) (jvm aload 5))
         ((= (x) 39) (jvm astore 3))
         ((= (x) 40) (jvm goto 13))
         ((= (x) 41) (jvm aload 3))
         ((= (x) 42) (jvm ifnull 57))
         ((= (x) 43) (jvm aload 0))
         ((= (x) 44) (jvm getfield times (COS_JHashMap)))
         ((= (x) 45) (jvm aload 3))
         ((= (x) 46) (jvm new (java lang Integer)))
         ((= (x) 47) (jvm dup))
         ((= (x) 48) (jvm aload 0))
         ((= (x) 49) (jvm getfield now (int)))
         ((= (x) 50) (jvm invokespecial <init>-I-V 1 0))
         ((= (x) 51) (jvm invokevirtual put-Object-Object-V 2 0))
         ((= (x) 52) (jvm aload 0))
         ((= (x) 53) (jvm aload 3))
         ((= (x) 54) (jvm aload 1))
         ((= (x) 55) (jvm invokevirtual apply-COS_JRoom-COS_JRoom 1 1))
         ((= (x) 56) (jvm invokevirtual setNextRoom-COS_JRoom-V 1 0))
         ((= (x) 57) (jvm aload 0))
         ((= (x) 58) (jvm dup))
         ((= (x) 59) (jvm getfield now (int)))
         ((= (x) 60) (jvm iconst 1))
         ((= (x) 61) (jvm iadd))
         ((= (x) 62) (jvm putfield now (int)))
         ((= (x) 63) (jvm return))
         (jvm return))
   )

   (method update (self update-V))

 ;

66. test JRoom, JDoor, JThing, etc

define s (? x / String new int-init / x);

define room1 (COS_JRoom new <init>);

define room2 (COS_JRoom new <init>);

define door12 (COS_JDoor new <init> 
              (room1) (s "south") (room2) (s "north"));

define jworld (COS_JWorld new <init>);

define thing1 (COS_JThing new <init>);

define robo1 (COS_JRobo new <init>);

act / jworld add (thing1) / s "bus";

act / jworld add (robo1) / s "autobus";

act / jworld add (room1) / s "boston";

act / jworld add (room2) / s "newyork";

begin (room1 get add (room1))
       (= 1 / room1 get size);

= 1 / room1 get size;

= 0 / room2 get size;

act / thing1 setRoom (room1);

= 2 / room1 get size;

= 0 / room2 get size;

act / thing1 setRoom (room2);

room1 get size;

room2 get size;

thing1 equals (thing1);

room1 equals (room1);

not / thing1 equals (room1);

(equal "newyork" / door12 apply (room1) (s "south") getName intValue);

(equal "boston" / door12 apply (room2) (s "north") getName intValue);

define o
  (? x / jworld get / s / x);

= "newyork" / (o "bus") getRoom getName intValue;

act / robo1 setRoom (room1);

(equal "boston" / (o "autobus") getRoom getName intValue);

act / jworld update;

(equal "newyork" / (o "autobus") getRoom getName intValue);